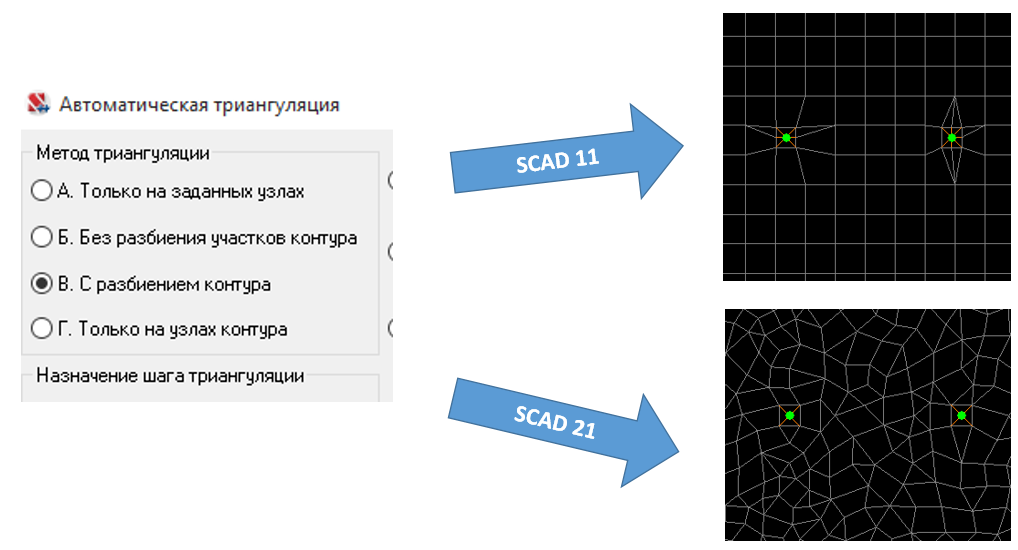
Как известно, в 21 версии СКАДа появился новый вид автоматической триангуляции плоских контуров. Если ранее программа старалась бить сетку на квадраты, не обращая внимания на вырождающиеся вытянутые элементы, то сейчас автоматическая сетка выглядит треугольной, хаотичной, но более-менее равномерной. Насколько это хорошо или плохо, я и попытался рассмотреть.
Описание экспериментальных моделей
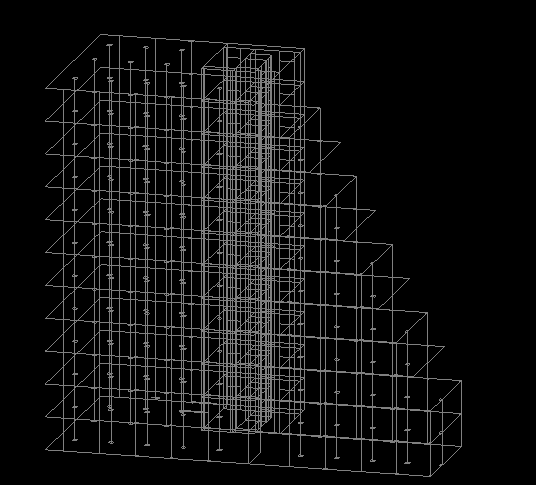
Для рассмотрения сеток на конкретном примере была выбрана часть здания с переменным по высоте планом. В выбранной модели плиты перекрытия имеют разный размер и форму, что позволило выловить больше возможных "косяков" и ошибок при создании сеток КЭ. Заготовка модели состояла из контуров плит и стен, а также осей колонн и площадок сопряжения колонн с перекрытиями.
Модель была дважды разбита на конечные элементы с ручным выделением каждого контура. Первый способ - "В. С разбиением контура" - для получения неортогональной "треугольной" сетки, второй - "Создание ортогональной сетки с заданным максимальным размером элемента" - для создания "старой" ортогональной сетки. Далее будем называть эти сетки просто "ортогональная" и "неортогональная".
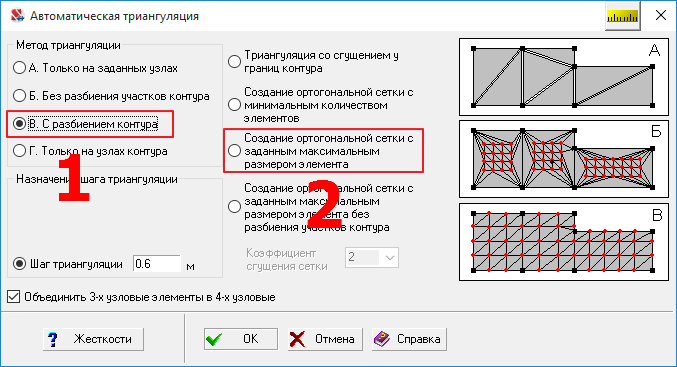
В обоих случаях шаг триангуляции был выбран равным 0.6 метра. Опытным путем (тестовыми разбиениями), а также с учетом общепринятых правил этот шаг был принят оптимальным. В обоих случаях был отмечен чекбокс "Объединить 3-х узловые элементы в 4-х узловые". SCAD не объединяет два треугольника в прямоугольник, если при этом снижается качество сетки. Из-за этого количество треугольников в модели с неортогональной сеткой оказалось существенно выше.
Полученные модели выглядели следующим образом:
Улучшение качества триангуляции - две дополнительные модели
Затем, задачу было решено расширить и включить в рассмотрение еще две модели - с улучшенной сеткой конечных элементов. Улучшение сетки производилось штатным средством SCAD 21.1.
О работе инструмента "улучшение качества триангуляции"
Инструмент улучшения качества триангуляции, согласно справке к программе, "производит попытку сместить те узлы, которые были порождены в процессе создания конечноэлементной сетки таким образом, чтобы улучшить показатели качества". Фактически, согласно моим наблюдениям (отчасти подтвержденным разработчиками), работает инструмент следующим образом:
- Узлы "неудовлетворительных элементов" (об оценке качества смотри ниже) передвигаются строго в плоскости тех пластин, которым они принадлежат.
- Если узел принадлежит пластинам, лежащим в другой плоскости - его программа не трогает.
- Если узел принадлежит каким-либо стержням или специальным конечным элементам - его программа не трогает.
Таким образом, использование инструмента целиком на всей модели не представляет видимой опасности и не искажает модель.
Обе созданные модели рассматривались в двух вариантах - до улучшения и после него. В результате рассматривалось 4 отдельных модели с различными сетками конечных элементов:
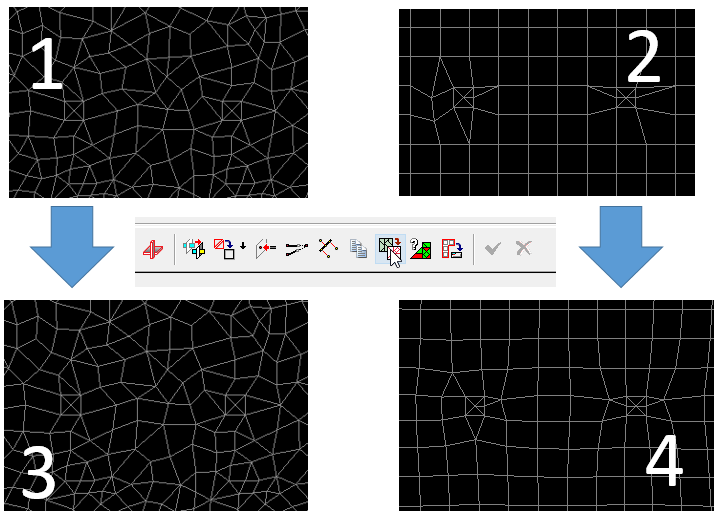
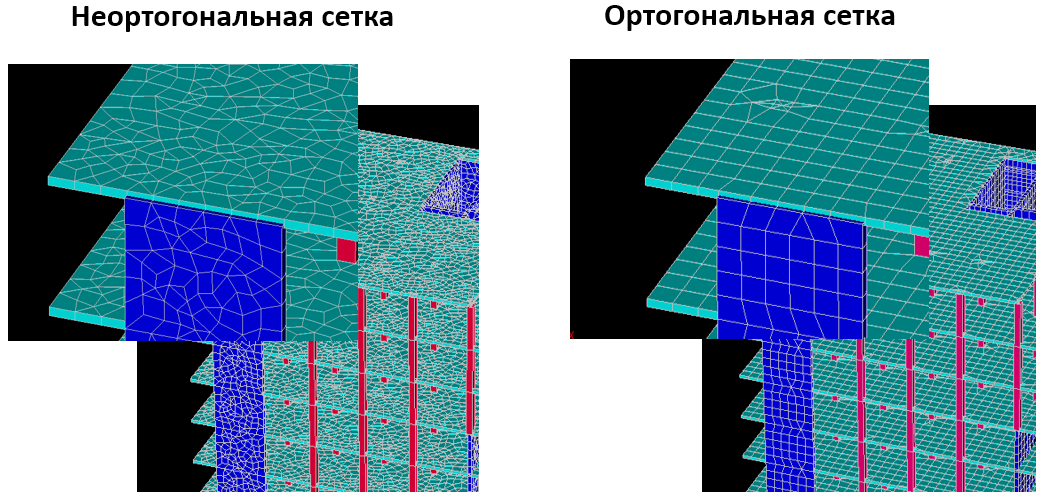
Полученные сетки КЭ
Полученные сетки КЭ на примере одной из плит перекрытия представлены ниже:
 Ортогональная сетка до улучшения
Ортогональная сетка до улучшения


Предварительный анализ
Первоначально полученные модели сравнивались численно - по количественным показателям. В том числе использовались показатели встроенного в SCAD 21.1 инструмента оценки качества.
О коэффициенте формы
Коэффициент формы элемента в SCAD - это отношение суммы квадратов сторон к 4 площадям этого элемента:
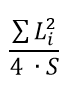
К примеру, для квадрата (вероятно, идеальной формой конечного элемента является именно квадрат) коэффициент формы будет равен 1. Для равностороннего треугольника - корень из 3.
upd: при этом для равностороннего треугольника в схеме SCAD дает коэффициент формы, равный 1. Спасибо Chardash за указание в сторону книги "Беседы о строительной механике" Перельмутера А.В, где на 99 странице есть таблица с оптимальными и рекомендуемыми параметрами конечных элементов,в том числе коэффициента формы. Правда и там Анатолий Викторович не объясняет, почему используется именно этот критерий, тем более, что получается, что формулы для треугольных и четырехугольных элементов, судя по всему, различаются, а значит критерий, вероятно, не универсален. То есть мы не можем сказать, что сетка из треугольников с коэффициентом формы = 1.2 лучше или хуже сетки четырехугольников с тем же коэффициентом формы.
Почему выбрана именно эта формула я определить не берусь. Каких-то научных трудов, где она упоминалась бы, я тоже найти не смог. Зато нашел другие варианты определения коэффициента геометрической формы плоской фигуры, например в этой статье коэффициентом формы называется несколько иная характеристика, выражающаяся через контурный интеграл. Для сравнения, коэффициент формы равностороннего треугольника и квадрата из приведенной статьи - 6 корней из 3 и 8 соответственно.
По умолчанию SCAD считает нежелательными элементами треугольные элементы с коэффициентом формы, превышающим 1.3 и четырехугольные - 1.4.
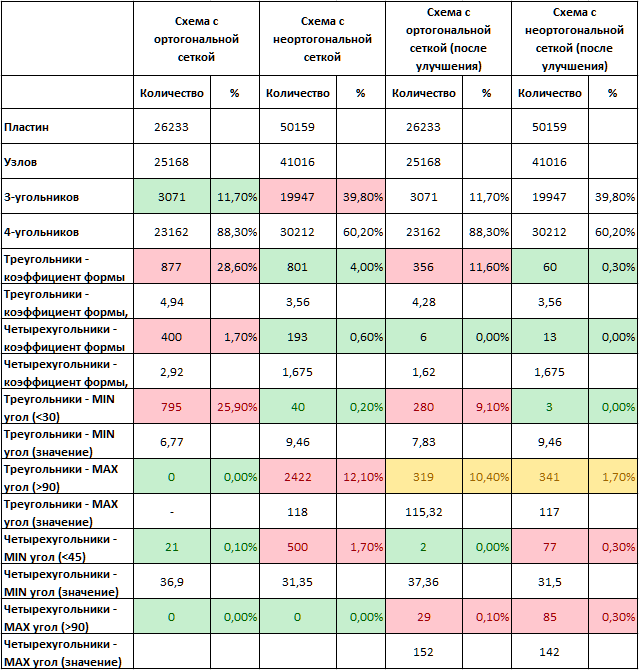
Выводы по предварительному анализу:
- Ортогональная сетка дает существенно меньшее количество элементов и узлов при одинаковом шаге разбиения.
- Ортогональная сетка дает существенно меньший процент треугольных КЭ. Ортогональная сетка изначально создается из прямоугольных треугольников, которые изначально предназначены для объединения в прямоугольники.
- Неортогональная сетка дает меньше "неправильных" элементов. Объяснимо тем, что она изначально создается по правилам, которые позволяют почти все элементы
- Улучшение качества триангуляции дает ощутимое снижение "неправильных" элементов. То есть только на основании цифр из этой таблицы можно рекомендовать этот инструмент к использованию.
Загружения
Все 4 модели были загружены одинаковым набором нагрузок:
- Собственный вес элементов
- Кратковременная равномерно распределенная на плиты (2.4 кПа)
- Длительная равномерно распределенная на плиты (1.8 кПа)
- Ветер в "левый" торец здания (после разбиений на всех 4 моделях узлы этого торца оказались распределены с постоянным шагом, что дало возможность приложить ветровую нагрузку в виде трапециевидной, приложенной к узлам):

- Модальный анализ. Псевдозагружение, используемое для определения собственных частот модели.
Были сформированы одинаковые исходные данные для РСУ и комбинация L1+L2+L3+L4 для всех моделей.
Линейный расчет
| Cхема с ортогональной сеткой | Схема с неортогональной сеткой | Схема с ортогональной сеткой (после улучшения) | Схема с неортогональной сеткой (после улучшения) | |
| Порядок системы уравнений | 151008 | 246096 | 151008 | 246096 |
| Необходимое количество оперативной памяти |
380.5 Mb |
503.4 Mb | 380.5 Mb | 503.4 Mb |
Выводы:
- Очевидно, так как модель с разбиением неортогональной сеткой имеет большее число элементов и узлов, то и машинных ресурсов на неё затрачивается больше.
- Улучшение качества триангуляции никак не влияет на ресурсоемкость задачи, так как не изменяет числа элементов и/или узлов, лишь передвигая их.
Модальный анализ
Периоды собственных колебаний по первым 4 формам представлены в таблице:
| Cхема с ортогональной сеткой | Схема с неортогональной сеткой | Схема с ортогональной сеткой (после улучшения) | Схема с неортогональной сеткой (после улучшения) | |
| Форма 1 | 2.1428 | 2.1048 | 2.1439 | 2.1056 |
| Форма 2 | 1.4942 | 1.4894 |
1.4952 |
1.4906 |
| Форма 3 | 0.6327 | 0.6326 | 0.6327 | 0.6326 |
| Форма 4 | 0.5297 | 0.5235 | 0.5298 | 0.5235 |
Выводы:
- Так как при автоматическом распределении масс SCAD массы всех элементов распределяет между их узлами, то чем мельче будут элементы в модели, тем более равномерным будет распределение масс.
- Даже в моделях с одинаковым шагом триангуляции контуров разница периодов (а, соответственно, и частот) собственных колебаний составила до 2%. При более редком разбиении, очевидно, ошибка определения собственных частот будет только возрастать.
Поля напряжений в плитах
После линейного расчета были рассмотрены поля напряжений. Приводить огромное число картинок не вижу смысла, в конце статьи присутствуют ссылки на расчетные файлы - каждый может рассмотреть интересные поля самостоятельно.
Анализировать поля количественно не позволяют всплески - максимальные и минимальные значения полей напряжений приходятся именно на них. Качественно же, очевидно, картины напряжений не отличаются.
В качестве примера картины всплесков напряжений привожу картину Mx на одной из плит возле одной и той же колонны:
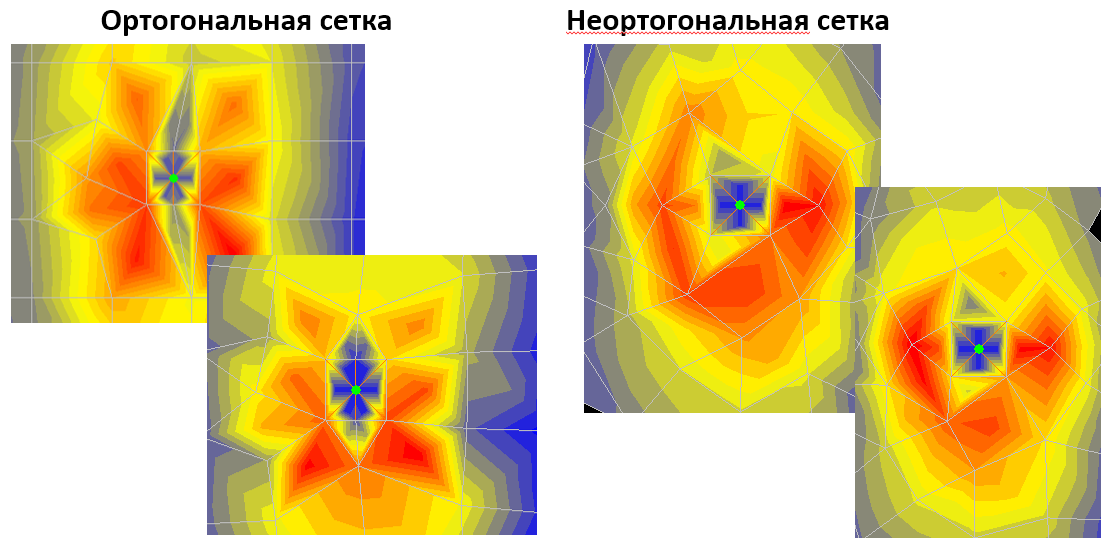
Как видно - неортогональная сетка в данном случае не помогла избавиться от всплеска напряжений. Мало того, численно в показанных КЭ напряжения в неортогональной сетке оказались даже выше. Но при этом форма полей напряжений в данной области в неортогональной сетке заметно лучше - видны эллипсоидные изолинии, равномерно расходящиеся от колонны, в то время как в ортогональной сетке форма полей гораздо более хаотична и непрозрачна.
Рассмотрим другую колонну, на этот раз крайнюю:
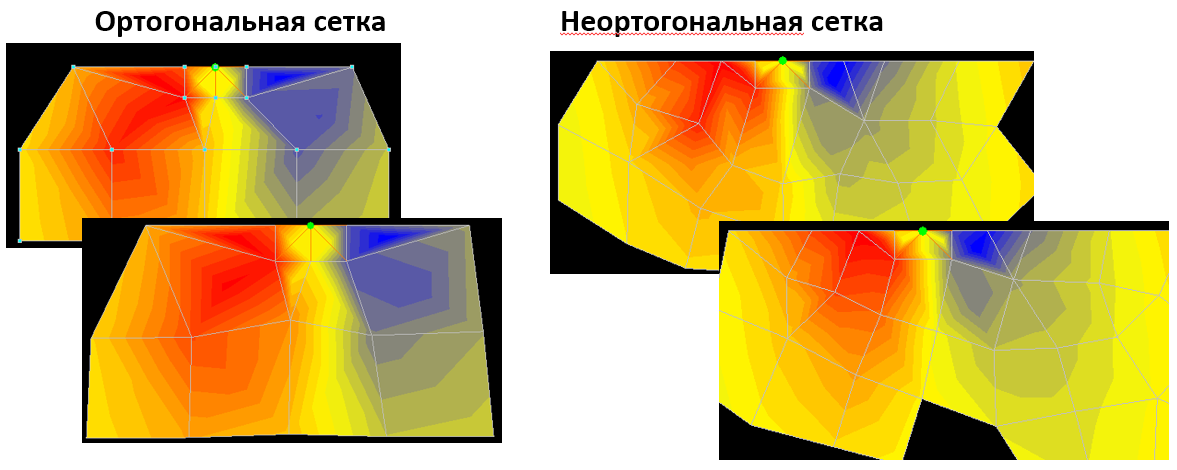
Опять форма полей напряжений в неортогональной сетке не идеальна (концентратор напряжений слева от колонны смещен к соседнему узлу, что явно неверно), но субъективно общая форма изолиний кажется более прозрачной и понятной, особенно на "улучшенной" сетке (нижнее изображение).
Есть и пример, где всплеск напряжений на неортогональной сетке практически не проявился:
Армирование плит
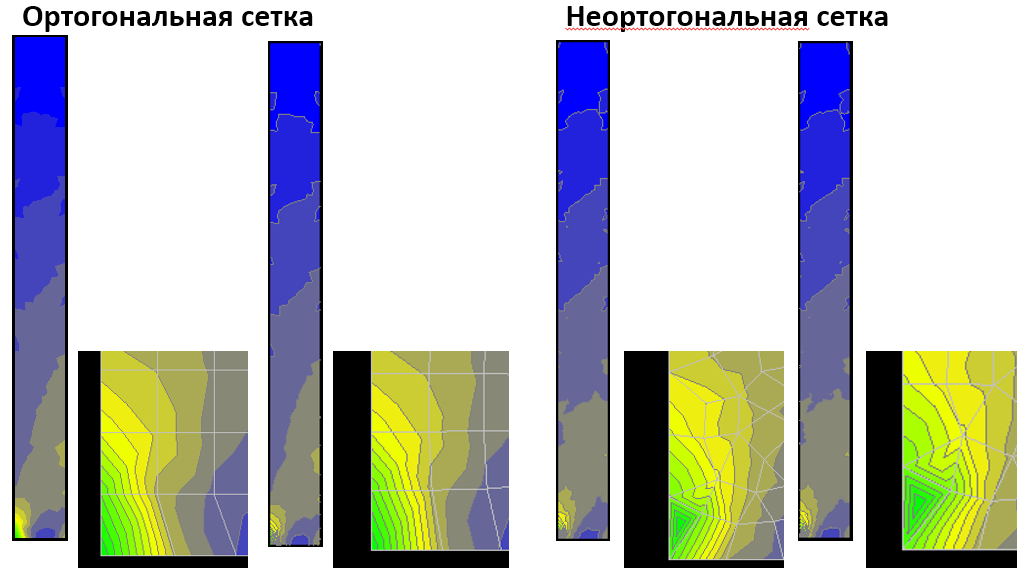
Исходные данные для групп армирования и РСУ были заданы одинаковыми. Нагрузки были заданы близкие к реальным для подобного типа зданий.
Приведены одинаковые участки одной и той же плиты в разных моделях. Картинки сверху - модели до улучшения сеток КЭ, внизу - после. Армирование верхнее по горизонтальному (на рисунке) направлению. Фоновая арматура принята одна и та же для всех схем, рассмотрено дополнительное армирование.


Выводы:
- Численные значения напряжений и получаемого армирования в целом по соответствующим элементам здания практически идентичны.
- В моделях, где присутствуют вытянутые треугольники, зоны допармирования также сильно вытягиваются.
- Сами же вытянутые треугольники, так как в них появляются концентраторы всплесков напряжений, SCAD армировать отказывается, вследствие чего у неопытного пользователя может возникнуть ощущение, что, например, в данной плите необходимо применять капители или же увеличивать толщину плиты.
- Улучшение качества триангуляции, хоть и не дает возможности избавиться от всех вытянутых "красных" треугольников, позволяет существенно выровнять картину армирования.
- Хоть общая картина армирования в модели с неортогональной сеткой и выглядит лучше, но в ней присутствуют небольшие конечные элементы со всплесками даже там, где в модели с ортогональной сеткой всплески отсутствовали.
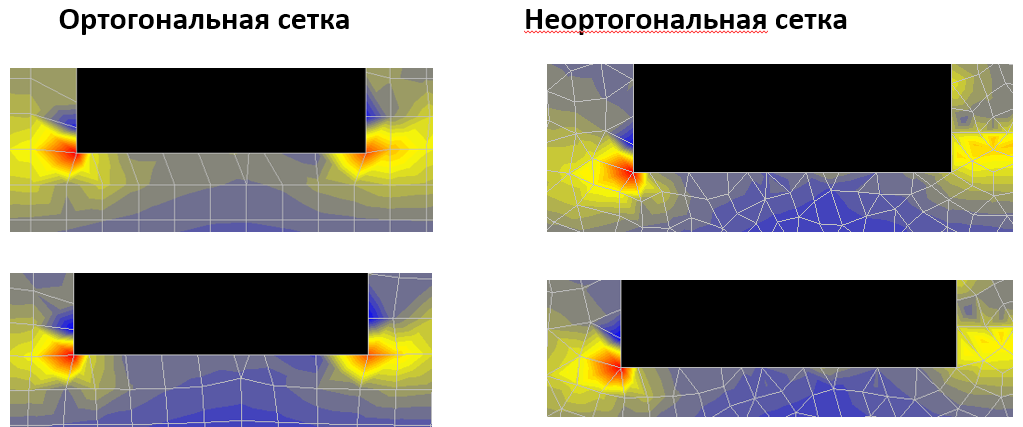
Поля напряжений в стенах
Рассматриваем напряжения Nx в стенах модели:
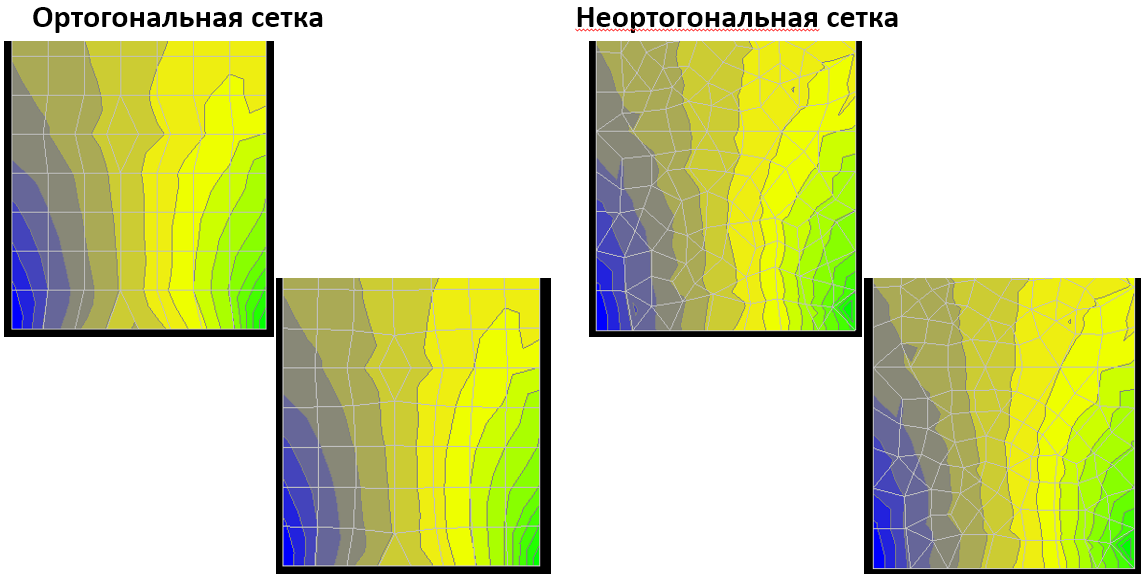
Выводы:
- Так как стены зачастую имеют более регулярную форму, то ортогональная сетка прекрасно справляется с разбиением стен на равномерные прямоугольные элементы без треугольных включений и "неправильных" конечных элементов. В таких условиях ортогональная сетка работает, по субъективным ощущениям, лучше, выдавая более равномерные изолинии с концентраторами напряжений в углах стен, а не в центрах конечных элементов.
Общие выводы
Не берусь утверждать, что открыл что-то новое для читателей и уж тем более не берусь давать каких-либо советов. При этом надеюсь, что на частый вопрос пользователей: "зачем в 21 версии скада ввели эту ужасную сетку" ответ я дал как минимум частично.
Использованные модели
Ортогональная сетка после улучшения



Комментарии
Авторизоваться
К картинкам где сравниваются напряжения надо добавить палитру с численными значениями напряжений для 1 и 2 варианта.
http://eurocodesguide.blogspot.ru/2015/08/blog-post_27.html