Итерационный алгоритм РСУ со снижением машиноёмкости перебора сочетаний

Предлагаю алгоритм определения РСУ в линейных упругих системах со сниженной машиноёмкостью подбора РСУ.

Предлагается только идея для разработчиков программ для расчётов. Возможности реализовать и проверить её не имею, так как программирую только в екселе, а тут надо серьёзное программирование.
Современные процессоры типа интел i3 с производительностью около 36,8 Гфлоп/с выполняют примерно стлько же операций деления в с (37*10^9 операций/с).
Согласно комбинаторике перебор РСУ из более чем 17 усилий даст 3,55687E+14 вариатов и для такого процессора займёт 2,7 часа, а уже 18 усилий дадут 6,40237E+15 вариантов и займут 48 часов. При этом в расчётеах комбинаторики используются факториалы, которые известны тем, что это одна из наиболее быстро растущих функций.
Таким образом перебором получить РСУ для более чем 17 усилий сегодня в реальных условиях невозможно.
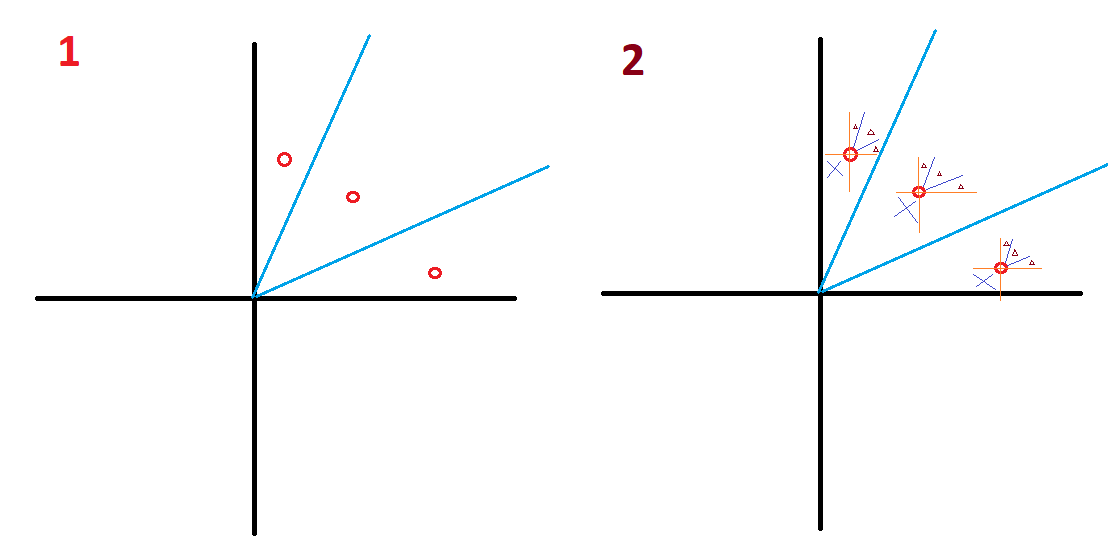
Представим все возможные РСУ в виде 3 трёхмерных фигур и 2 двухмерных.
Перечислим эти фигуры:
1) N, Мх, Му - нормальные напряжения, опрокидывание, продольное армирование;
2) Qx, Qx, Мкр - касательные напряжения, устойчивость стенок, поперечное армирование;
3) N, Qx, Qx - простой сдвиг по трению по грунту;
4) N, касательные напряжения (с учётом кручения) - двухмерная звезда, для сложных случаев, когда потребуется учитывать трение с учётом кручения (на сегодня невостребовано, но в будущем вероятно это будет актуально).
5) нормальные, касательные напряжения - двухмерная звезда, для сложных случаев, когда потребуется учитывать трение с учётом изгиба и кручения (на сегодня невостребовано, но в будущем вероятно это будет актуально).

Для наглядности назовём такие фигуры новым термином "звезда РСУ".
Можно доказать, что при получении точки для вершины такой звезды, при снижении любой нагрузки на 5...10% или на бесконечно малую величину точка вершины будет прижиматься к центру координат, а не возвышаться ещё опасней. Таким образом вершины будут представлять собой острые углы при точном расчёте уменьшения нагрузок. Таким образом, в запас, можно считать вершины прямыми углами от вершины перпендикулярно осям координат (N, Мх, Му).
Такие фигуры будут представлять собой не сплошное тело, а тело с полостями.
Полости ввиду отсутствия опасности от них не изучаются. Например для трёхмерного тела N, Мх, Му для опрокидывания опасным будет сочетание Nmin, Мхmax, Муmax, однако это "поверхность сегмента" огибающая вершины фигуры в областях с Nmin, а не полость внутри фигуры.
Для пластин добавятся Мху и прочие факторы, но в статье пока не рассматриваются пластины, а только стержни. Перейти со стержней на пластины будет несложно, просто добавив несколько измерений звёздам РСУ.

Несложно подобрать алгоритм для анализа всей фигуры после перебора всех возможных РСУ.
Однако перебор всех РСУ современными техническими средствами оказывается невозможен из-за значительной машиноёмкости, продолжительности расчёта.
При этом получить звезду РСУ иначе, чем перебором вариантов сочетаний, не представляется возможным.
Иной путь - развитие экстрасенсорных способностей у компьютеров или нормирование не нагрузок, а сразу сочетаний (например проектирование путём копирования моделей как в средневековье), что сейчас невозможно.
Значимость приобретают методы уменьшения вариантов перебора сочетаний.
Часть этих методов уже придумана и внедрена в современные программы МКЭ типа SCAD.
В статье предлагается усовершенствование подобных методов путём итераций от значимых усилий к наиболее слабо влияющим на результат.

Обычная часть, стандартная для всех программ. Можете пропустить.
Исходные данные.
1) Определяются исходные данные - усилия от нагрузок.
2) Усилия делятся на постоянные, длительные, кратковременные, особые по своим нагрузкам.
3) Усилиям назначаются коэффициенты надёжности по нагрузке.
4) Усилиям назначается объединение, взаимоисключение, сопутствие, знакопеременность по аналогии со SCAD, Лира и т.п.
5) Вводится новое понятие "знакопеременный характер".
Например, ветер по одной оси можно задать одним усилием с учётом +- знакопеременности.
Однако тот же ветер можно задать и двумя разными усилиями (с юга и с севера), но программа этого не знает. Чтобы сообщить программе о том, что это взаимоисключающие псевдознакопеременные нагрузки добавляется новый термин "знакопеременный характер".
Использовать данный термин можно при выделении сочетаний, что уточнит РСУ. Например, все 4 ветра должны учитываться в определённых РСУ.
6) Вводится природа усилий по СП 20 аналогично SCAD, Лире. Снег, ветер, торможение крана и т.п.
Использовать это можно при выделении сочетаний, что уточнит РСУ.
7) Вводится доля длительности каждому усилию. Таким образом получается РСУ из пониженных нагрузок для прогибов, осадок и т.п.
8) Каждому усилию назначается вклад в общий НДС.
Предлагается вклад = усилие / максимальное усилие (+). Так же рассматриваются вклад = усилие / минимальное усилие (-).
Вклад назначается по каждому силовому фактору N, Мх, Му, Qх, Qу, Мкр.
Для каждого усилия-нагрузки получается по 6 вкладов.
В дальнейшем усилия оцениваются по каждому вкладу отдельно.
9) Каждому усилию автоматически, согласно СП 20, вводятся возможные коэффициенты сочетаний 0,7; 0,85; 0,9; 1 в зависимости от длительности, величины вкладов.
*******
10) Из вышеизложенных исходных данных получаем виды усилий для подбора сочетаний.
Виды усилий:
нормативные усилия / коэффициент надёжности по нагрузке = расчётные усилия для опрокидывания и т.п.
нормативные усилия
нормативные усилия * коэффициент надёжности по нагрузке = расчётные усилия
11) Каждое из усилий можно умножать на разные коэффициенты сочетаний получая сочетания.
Далее обычным перебором можно получать все звезды РСУ (коих я насчитал 5 штук х 5 = 25 штук):
нормативные/коэф. надёжности по нагрузкам полная;
нормативные полная;
нормативные постоянные + длительные=пониженная;
расчётные полная;
расчётные постоянные + длительные=пониженная.
И так для 3 факторов N, Мх, Му и отдельно для Qx; Qx, Мкр.
12) Для надёжности страхуемся самым популярным методом - перебор суммированием и вычитанием всех усилий (при взаимоисключении принимаются усилия с наибольшим вкладом по нормальному или касательному напряжению).
По каждой звезде так получается 8х3+4х2=24+8=32 сочетаний по нормальным напряжениям или 8 сочетаний по касательным напряжениям.
Данные сочетания не будут самыми опасными.
Данная операция направлена на добавление надёжности, в случае, если следующий предлагаемый метод ввиду новизны даст ошибку.
13) Для надёжности страхуемся самым популярным методом - к постоянным усилиям прибавляем по одному (а в случае объединения или сопутствия усилий, все такие усилия) усилию по каждому усилию. Получается около 40-80 сочетания для типовых случаев.

Новое.
*******
Идея основана на учёте вклада усилия в сочетание.
Предлагается звёзды РСУ строить при помощи итераций.
Сначала строятся звёзды учитывающие только усилия с наибольшим вкладом.
Далее эти звёзды анализируются и выделяются наиболее опасные вершины-сочетания.
Далее на эти вершины-сочетания надеваются всё более мелкие усилия с циклами повторения.
В частности предлагается такой порядок.

13) Все усилия делятся на группы по вкладу по каждому силовому фактору.
Выделяются группы с вкладом по каждому усилию 0-20%, 20-40%, 40-60%, 60-80%, 80-100%.
То есть каждое усилие получает 6 групп по каждому силовому фактору. При этом велика вероятность, что при малом вкладе по одному фактору, по прочим факторам вклад также будет малым. Эта вероятность и позволит методу уменьшить машиноёмкость и отсечь бОльшую часть перебора вариантов сочетаний.

14) Строятся первые зачатки звёзд с вкладом 60-100%.

15) Звёзды в своих координатах делятся на сектора, по 9 секторов (для трёхмерных звёзд) на одну восьмую часть пространства (и по 3 для двухмерных).
Здесь нужно дополнительное исследование. Возможно, таким образом будут отсечены самые опасные сочетания по отрыву/опрокидыванию при Nmin. Возможно, потребуется добавление лишних 6 секторов ближе к осям. Однако добавление лишних секторов в каждой восьмой части приведёт к увеличению машиноёмкости. Также велика вероятность, что эти лишние сектора добавят величину сочетаний менее инженрной точности (которую для 21 века можно считать как 1%).
Также можно регулировать вероятность отсечения опсных сочетаний у осей наклоном крайних секторов относительно осей.
Нужны дополнительные исследования машиноёмкости и вероятности отсечения опасных сочетаний для реальных объектов.

16) По каждому сектору для каждой вершины определяется радиус-вектор из нуля координат.

17) Принимается, что наиболее опасное сочетание в каждом секторе будет иметь наибольший радиус-вектор.

18) Таким образом остаются 8х9=72 опасных сочетаний в каждой трёхмерной звезде (а звёзд всего 3). Или 4*3=12 опасных сочетаний для двух двухмерных звёзд.
Всего 72*3*5+4*3*2*5=1200 сочетаний.

19) Далее начинается следующая итерация.
На выявленные опасные вершины добавляются усилия в вкладом по каждому фактору 40-60%.
Вокруг первоначальных вершин появляются свои минизвёзды. Каждой вершине такой минизвезды определяется радиус-вектор от изначальной вершины. Каждому радиус-вектору определяется проекция такого радиуса вектора на радиус-вектор от изначальной вершины до нуля координат.
Добавляются дополнительные координаты для каждой изначальной вершины.
В этих новых дополнительных координатах назначаются по 9 секторов в каждой восьмой части пространства, кроме той, что направлена к изначальному нулю координат.
По сумме изначального радус-вектора + проекция определяются самые опасные новые вершины минизвезды.
У каждой минизвезды получается 9*7+3*3=72 вершин для каждой звезды РСУ.
Изначально было 1080+120=1200 изначальных опасных вершин.
1080 * 63=68040
120 * 9 = 1080
Всего 69120 опасных сочетаний.

20) Далее начинается следующая итерация.
На выявленные опасные вершины добавляются усилия в вкладом по каждому фактору 20-40%.
Получается следующие микрозвёзды на вершинах минизвёзд.
Получается
68040 * 63 = 4286520
1080 * 9 = 9720
Всего 4 296 240 опасных сочетаний.

21) Далее начинается следующая итерация.
На выявленные опасные вершины добавляются усилия в вкладом по каждому фактору 0-20%.
Получается следующие нанозвёзды на вершинах микрозвёзд.
Получается
4286520 * 63 = 270050760
9720 * 9 = 87480
Всего 270 138 240 опасных сочетаний.

22) Принимается, что опасные сочетания с учётом инженерной погрешности менее 1% все учтены.
Тут, конечно, есть вопросы к проценту погрешности и вероятность пропуска опасных сочетаний близко к погрешности за счёт деления пространства звёзд на ограниченное число секторов.
При достойной машиноёмкости метода менее 1 минуты, в принципе, ничто не мешает поделить квадранты на большее количество секторов (или сделать сектора под острым углом к осям не увеличивая машиноёмкость).

23) Далее из опыта анализа РСУ и составления сочетаний вручную можно сказать, что примерно
25% усилий с вкладом более 60%;
25% усилий с вкладом 40-60%;
25% усилий с вкладом 20-40%;
25% усилий с вкладом 0-20%.
Предположим, что анализируем сложный сарай, с общим числом усилий-нагрузок 52 штуки.
Простой перебор займёт 2,52309E+52 сут, короче никогда.

Каждую итерацию на вершины звезд будет прирастать простым перебором 6227020800 сочетания (от 52*0,25=13 усилий).
Перебор итерациями займёт:
1ая итерация 6227020800 сочетаний 0,168297859    с
из них остаются 1200 сочетаний.
2ая итерация 6227020800 * 1200 = 7,47242E+12 сочетаний 201,95 с
из них остаются 69120 сочетания
3я итерация 6227020800 * 69120 = 4,30412E+14 сочетаний 3,2 часа
из них остаются 4 296 240 сочетания
4ая итерация 6227020800 * 4 296 240=2,67528E+16 сочетаний 8,4 суток

Уже эти 9 суток на 51 порядок, чем простой перебор.
При помощи взаимоисключений и подобных фишек уверен, что продолжительность можно уменьшить вдвое.
В методе используется отсечение вершин последующих минизвёзд только в пределах вершины с углами 90 градусов.
Но можно пытаться отсекать и больше, допустим всё с отрицательными радиус-векторами к нулю координат. Тогда будет отсекаться куда больше новых вершин, примерно половина.
На общем числе сочетаний это скажется не как 0,5, а значительно сильнее. Тем самым продолжительность уменьшится ещё минимум вдвое.
Получится около 9/2/2=2 суток расчёта.

Конечно, это всё ещё очень много и не годится для реализации в программах непосредственно.
Но используя идею и подкручивая сектора, углы отсечения, число итераций, уверен, что можно выиграть ещё сколько-то машиноёмкости.
И, возможно, дойти до реальных 20 минут. Хотя бы для более простых сараев с 40 усилиями.

Возможно, что отсекая новые минивершины ещё жёстче удастся сократить машиноёмкость значительно больше, но уже рискуя погрешностью.

Идея предназначена для развития отечественного ПО.
Разрешается бесплатно использовать алгоритм в следующих отечественных продуктах: Лира Софт, программы для расчёта фундаментов ГИПРО, программа Фидесис, и прочих программах, если их собственники зарегистрированы и платят налоги на территории Российской Федерации и республики Беларусь.
Также разрешается использовать алгоритм в научных работах, собственных разработках, студенческих учебных работах ведущихся на территории Российской Федерации и республики Беларусь.
Использовать алгоритм для авторов ПО прочих стран запрещается.