Ключевые слова: прогрессирующее обрушение, пластический шарнир, progressive collapse, plastic hinge.
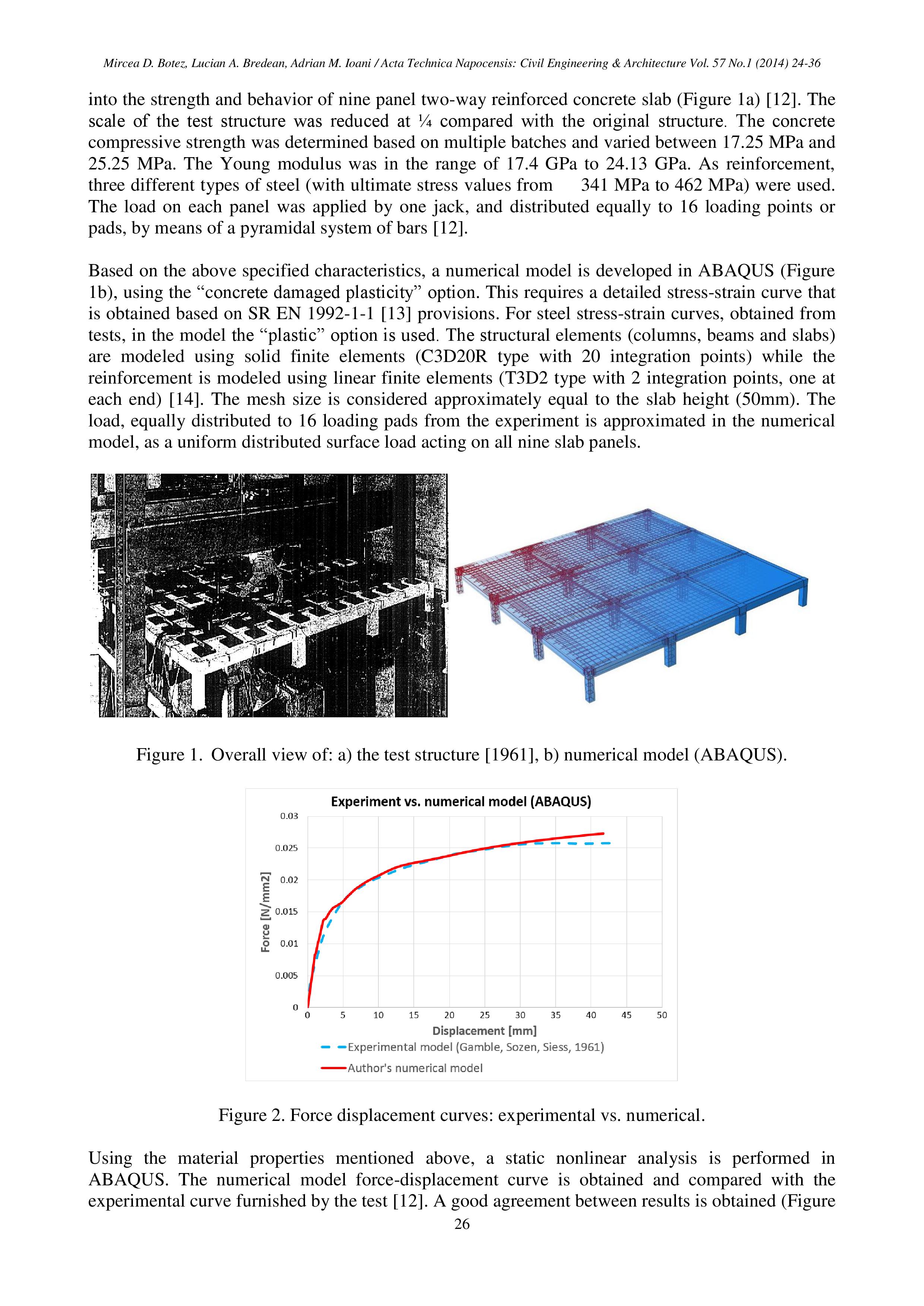
В этой заметке представлены характерные публикации зарубежных авторов, которые позволят читателям ознакомиться с одним из упрощенных методов учета физ. нелинейной работы конструкций. В соответствии с нормами США такой метод используется при сейсмических расчетах, pushover анализе, расчетах на прогрессирующее обрушение.
"Обычно" для учета физической нелинейности расчетчик задает в программном комплексе размеры сечений, параметры разбиения сечения на участки, диаграммы нелинейного деформирования материалов и т.д. Далее программа на каждом шаге нагружения обновляет жесткостные характеристики элементов.
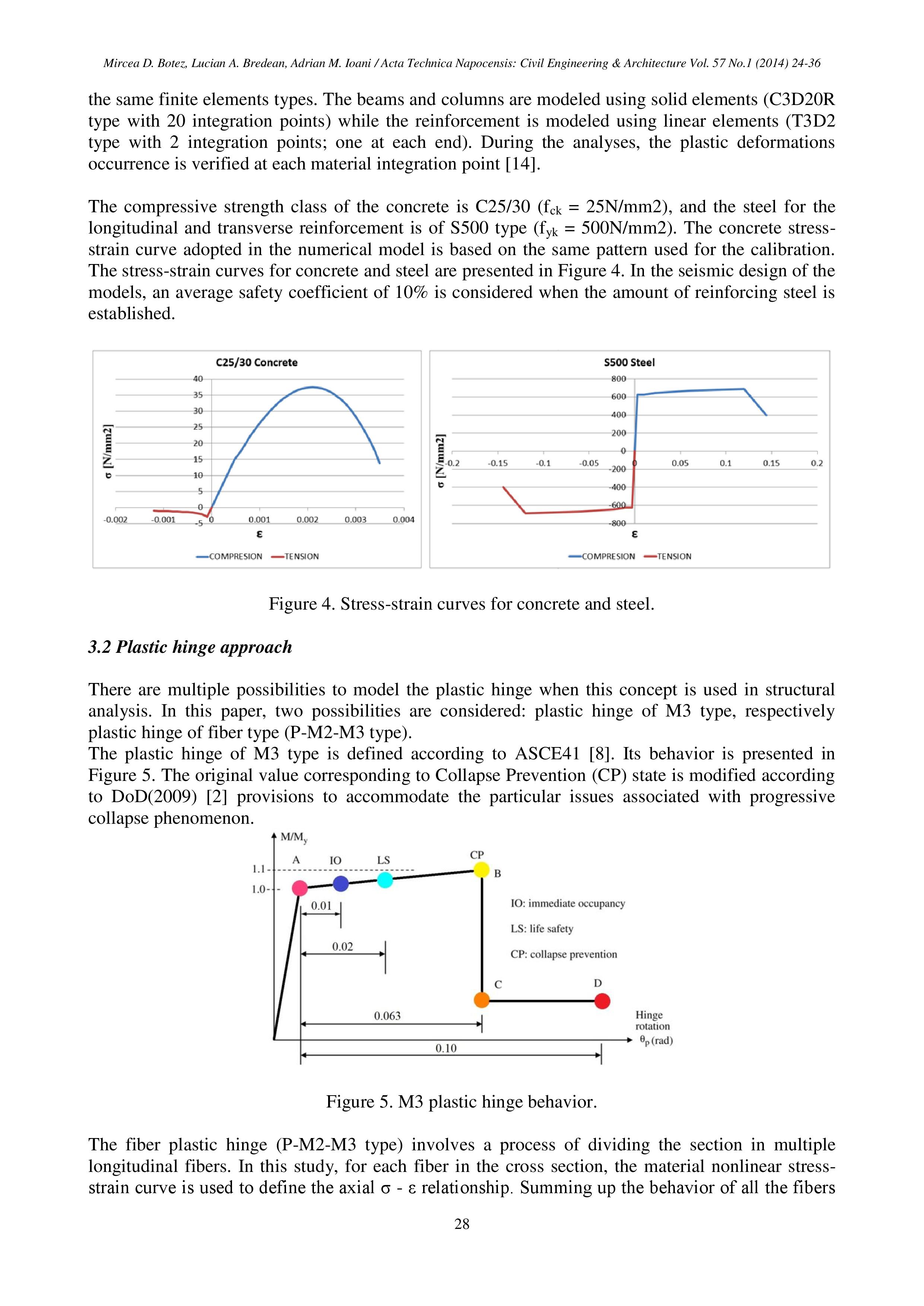
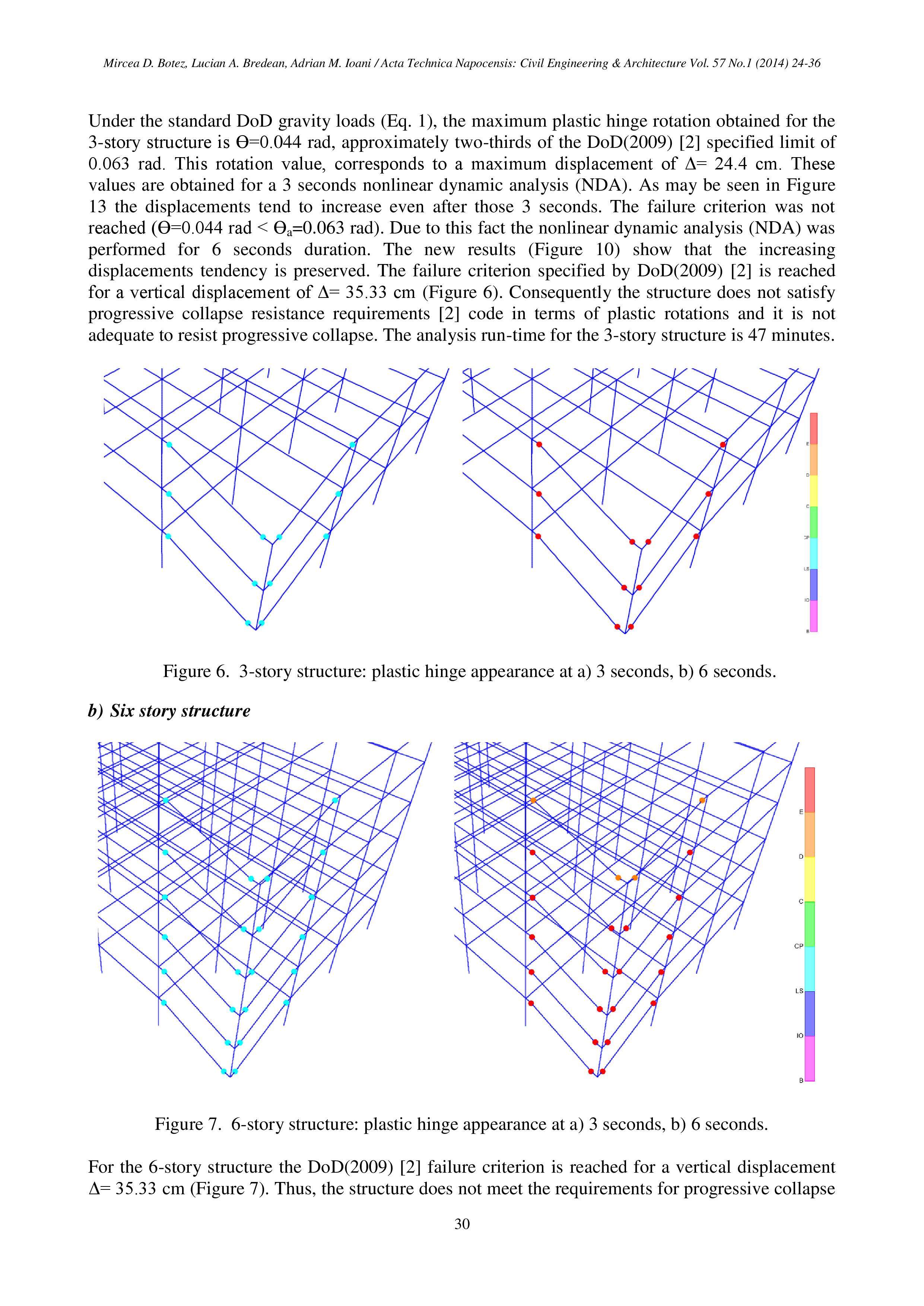
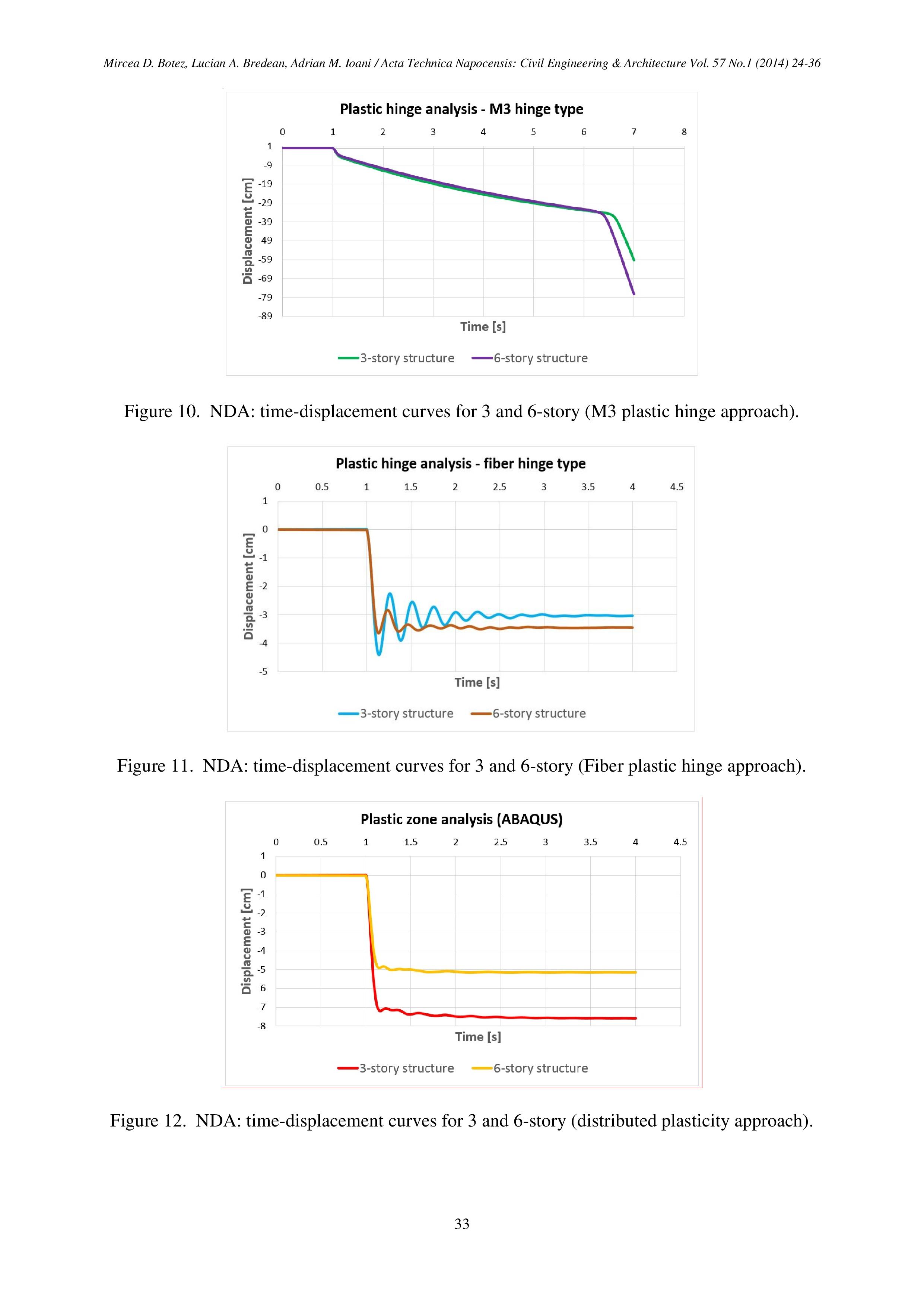
Альтернатива вышеприведенному подходу визуально напоминает метод предельного равновесия: в узлах сопряжения конечных элементов разных конструктивных элементов устанавливаются шарниры (или элементы связей, типа spring). Но шарниры не идеально-упругие конечной жесткости, а шарниры, поведение которых описывается нелинейной функциональной зависимостью между усилиями и деформациями (см. рис. 1). При этом материал конечных элементов задается физически линейным. В большинстве случаев шарниры задаются только по угловой степени свободы, «соответствующей» основному изгибающему моменту, действующему в сечении. В общем случае возможно использование «сложного» шарнира пластичности с отдельными «составляющими» для нормальной силы, поперечных сил и крутящего момента.

Рис. 1.1 – К моделированию пластического шарнира

Рис. 1.2 – Условный пример зависимости, описывающей поведение физнелинейного шарнира для изгибаемого элемента
Плюсы подхода:
- визуальная наглядность получаемых результатов;
- пользователь «контролирует», самостоятельно вычисляя и задавая в качестве исходных данных в расчетном комплексе величины предельных усилий, которые сечение воспринимает в упругой и пластической стадиях;
- для некоторых стран подход является нормативным (например, см. приложение "В" UFC 4-023-03, изд. 2013г., США);
- реализованность подхода в некоторых расчетных комплексах (например, Robot, SAP2000, Etabs).
Из минусов. Возникают вопросы:
- к достоверности подобного моделирования и соответствующих результатов при усилиях, близких к предельным;
- к учету фактора взаимного влияния усилий на предельные величины друг друга (например, значение предельного пластического момента Mпл, которое может воспринять сечение, зависит от величины нормальной силы N и пр.);
- к достоверности результатов по оценке устойчивости;
- достаточно ли для расчетов инженерной точности установки шарниров только по краям и середине конструктивного элемента или такие шарниры должны "активироваться" в любом сечении элемента, в котором усилия превышаеют величины, на границе между упругой и пластичной зоной работы и т.д. Если в вашей расчетной программе нет автоматического активирования шарниров, возможен "ломовой" подход, когда расчетчик искусственно ставит такие шарниры для каждого элемента;
- если в расчетный комплекс не встроена возмоность автоматического расчета предельных величин углов повора (или кривизн), то эти исходные данные нужно будет вычислять самостоятельно.
. . .
Вышеописанный метод с нелинейными шарнирами, реализованный в нормах США, разрабатывался и в СССР, но его область применения не ассоциировалась с расчетом на прогрессирующее обрушение (за исключением "ренессанса" в 2003-2012 гг.). Так можно посмотреть параграфы 13, 13.7 "Справочника по динамике сооружений" (Коренев Б.Г., Рабинович И.М., 1972г.). В этих параграфах рассматривается расчет сооружений на действие кратковременных нагрузок большой интенсивности. По своей сути рассмотренный в заметке №1 данного блога отказ опоры балки представляет собой импульсивную нагрузку R(t), которую можно охарактеризовать как мгновенную сосредоточенную нагрузку однократного действия, постоянного направления, имеющую не более одного максимума за время ее непрерывного действия tотк.
В параграфе 13.4 отмечается, что «Расчет конструкций на действие кратковременных динамических нагрузок производится по двум предельным состояниям. По первому предельному состоянию (по несущей способности) рассчитываются конструкции, к которым предъявляется следующее требование: конструкция должна выдержать однократное действие динамической нагрузки, полностью исчерпав свою несущую способность; при этом допускаются пластические деформации в материале конструкции, большие остаточные деформации и трещины. По второму предельному состоянию (по деформациям) рассчитываются конструкции, к которым предъявляются специальные требования по ограничению величин перемещений. При этом в конструкции могут допускаться или не допускаться пластические деформации.
В конструкциях, которые предназначены для многократного восприятия динамических нагрузок, пластические деформации, как правило, не допускаются.
Для изгибаемых и внецентренно сжатых с большим эксцентриситетом железобетонных конструкций достижение первого предельного состояния характеризуется началом разрушения бетона сжатой зоны в сечениях, в арматуре которых возникли пластические деформации (шарниры пластичности). Нормирование первого предельного состояния производится по величине полных углов раскрытия в шарнирах пластичности, а также по величине прогибов или по отношению полного прогиба к упругому (соответствующему началу текучести арматуры).
Условие прочности конструкции, в которой образовалось n шарниров пластичности, имеет вид: ψi<= ψni (i =1, 2, ..., n), где ψi – полученный из динамического расчета угол раскрытия в i-м шарнире пластичности; ψni – предельный угол раскрытия в i-м шарнире пластичности, принимаемый по графику рис. 13.7».

Рис. 13. 7 Предельные величины углов раскрытия в шарнирах пластичности
Из параграфа 13.5: «При расчете жестко-пластической конструкции она считается недеформируемой, пока усилия в каком-либо сечении не станут равными предельной величине и не возникнет возможность образования пластических деформаций. После этого начнется перемещение конструкции. Пластические деформации сосредоточены в шарнирах пластичности или на участках конечной длины, причём положение шарнира пластичности может меняться в процессе движения конструкции. Участки конструкции между шарнирами пластичности рассматриваются как жесткие. Полученные этим методом решения дают достоверные результаты лишь при больших пластических деформациях.
Основная трудность при использовании этих методов вызывается учетом движения пластических шарниров и пластических зон. Поэтому получают широкое распространение упрощенные методы, в которых шарниры или зоны пластичности считаются неперемещающимися в процессе деформирования конструкции (стационарными), а участки между ними принимаются жесткими».
Из параграфа 13.7: «Расчет балочных конструкций. Балка с идеальной жестко-пластической диаграммой деформации.
Балка считается неподвижной до тех пор, пока в каком-либо сечении изгибающий момент не достигнет предельной величины. После этого начинается движение по схеме абсолютно жестких стержней, соединенных пластическими шарнирами или пластическими участками конечной длины. Пластические шарниры могут быть стационарными (неподвижными) и нестационарными (перемещающимися по длине балки). Длины пластических участков могут меняться во времени.


Перед расчетом назначаются места расположения пластических шарниров, после чего определяется движение балки. Для проверки принятой расчетной схемы вычисляются изгибающие моменты, вызываемые действующей нагрузкой и силами инерции. Если величины изгибающих моментов меньше предельного значения или равны ему, то принятая расчетная схема правильна. Если же изгибающий момент на каком-либо участке балки превышает предельную «величину, то необходимо изменить расчетную схему: ввести нестационарные шарниры пластичности вместо стационарных; жесткие участки между нестационарными шарнирами заменить пластическими зонами и т.п.».
. . .
Ниже в развернутом виде выкладываются первые три публикации, которые в сочетании с другими работами, рекомендуемыми к ознакомлению, можно скачать по ссылке. Из относительно "свежих" русскоязычных источников, рассматривающих ж.б. конструкции, можно посмотреть, начиная с главы III, диссертацию Мехрализадех Алиреза «Конструктивная безопасность монолитных высотных зданий с переходными этажами при аварийных воздействиях» (МГСУ, 2014); при этом следует учитывать, что в этой работе не везде был успешно преодолен языковой барьер.
Также заслуживают внимание публикации:
Расторгуев Б.С. Обеспечение живучести зданий при особых динамических воздействиях. // Сейсмостойкое Строительство. Безопасность Сооружений, 2003, №4, с.45 -48.
Расторгуев Б.С., Мутока К.Н. Деформирование конструкций перекрытий каркасных зданий после внезапного разрушения одной колонны // Сейсмостойкое строительство. Безопасность сооружений, 2006. - №1.
. . .
статья № 1







статья № 2




статья № 3






ПЕРЕЧЕНЬ ВЫЛОЖЕННЫХ ПУБЛИКАЦИЙ
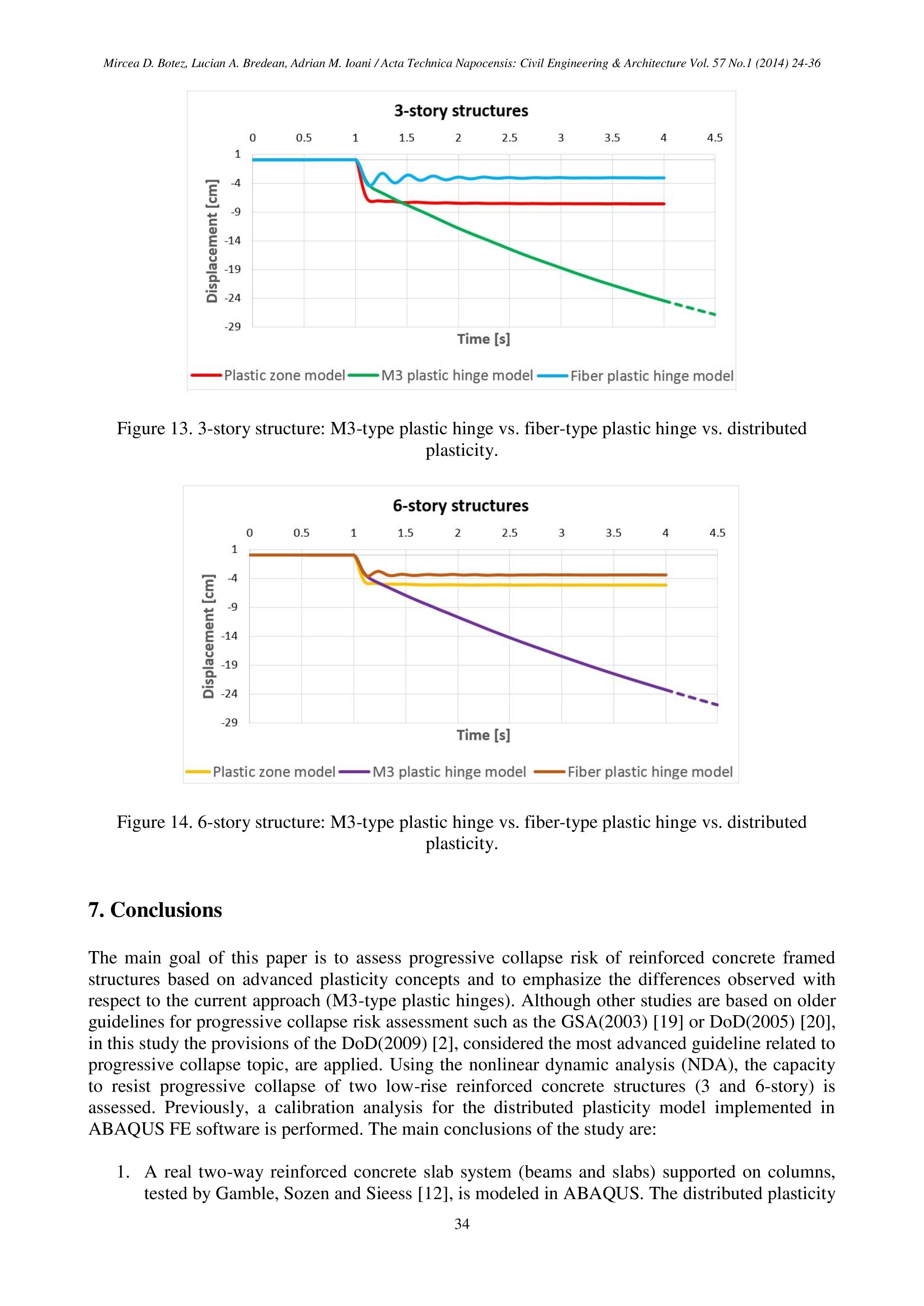
Статья 1. Mircea D. Botez, Lucian A. Bredean, Adrian M. Ioani. Plastic Hinge vs. Distributed Plasticity in the Progressive Collapse Analysis. Civil Engineering & Architecture Vol. 57, No. 1 (2014).
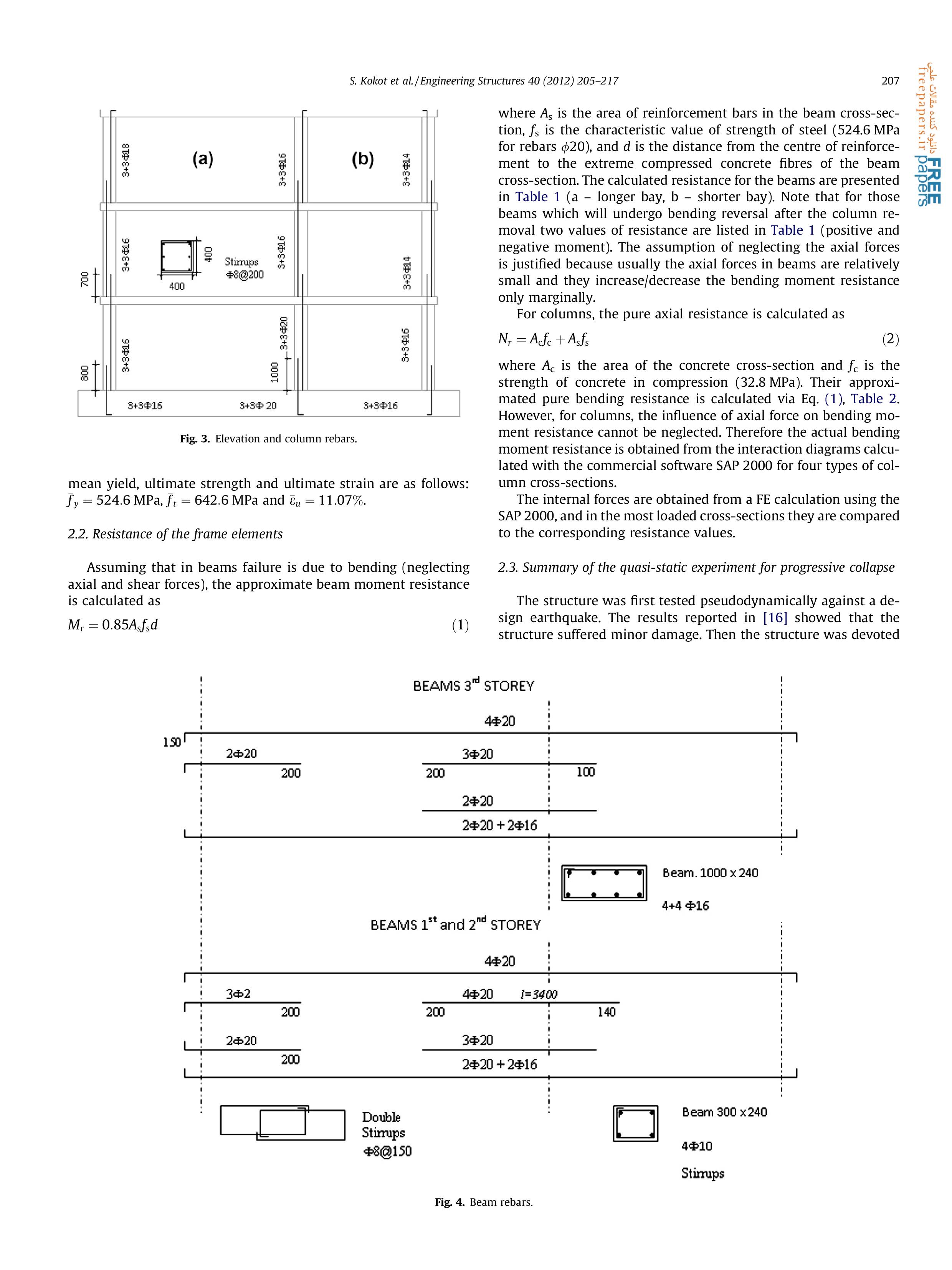
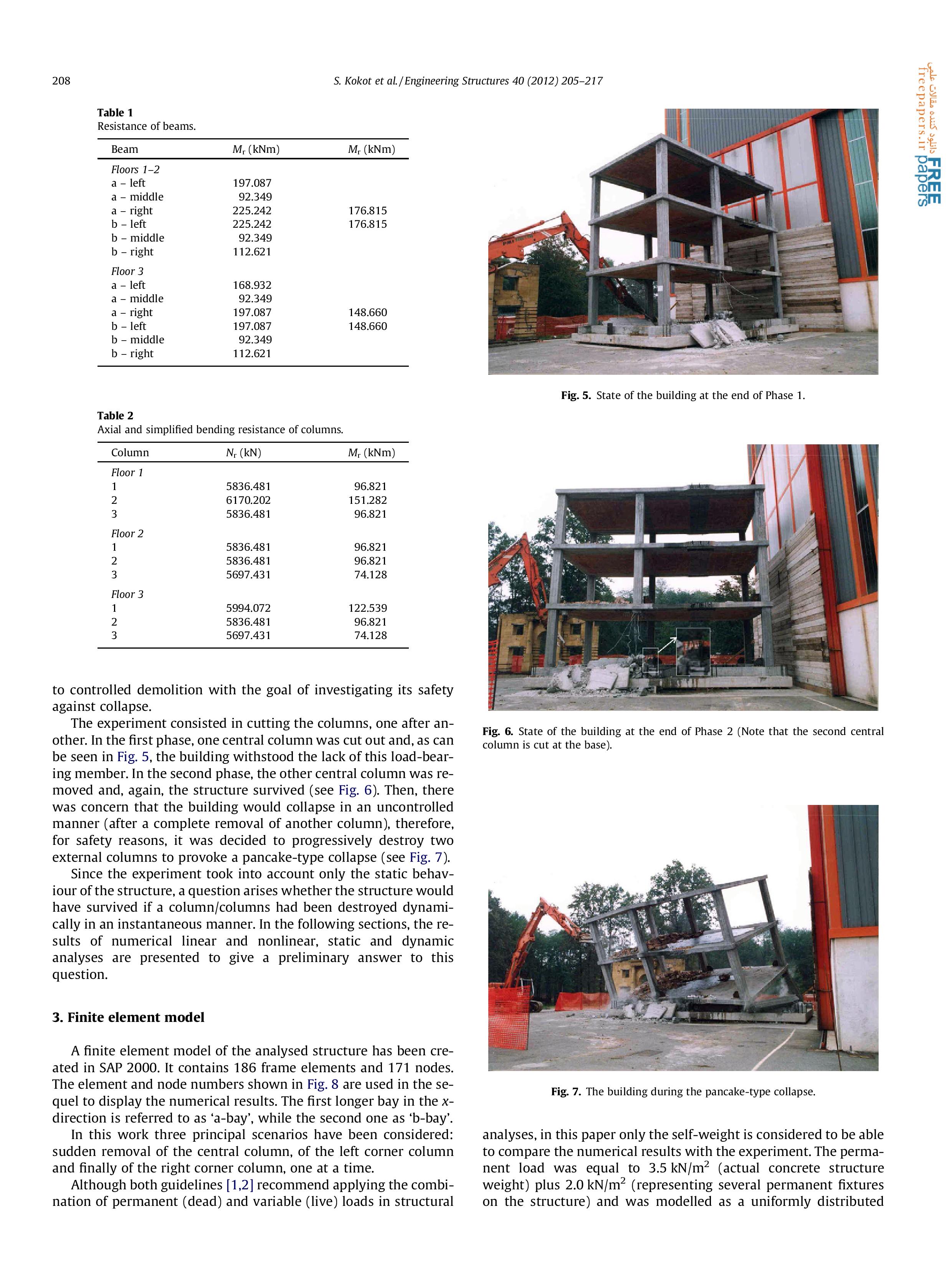
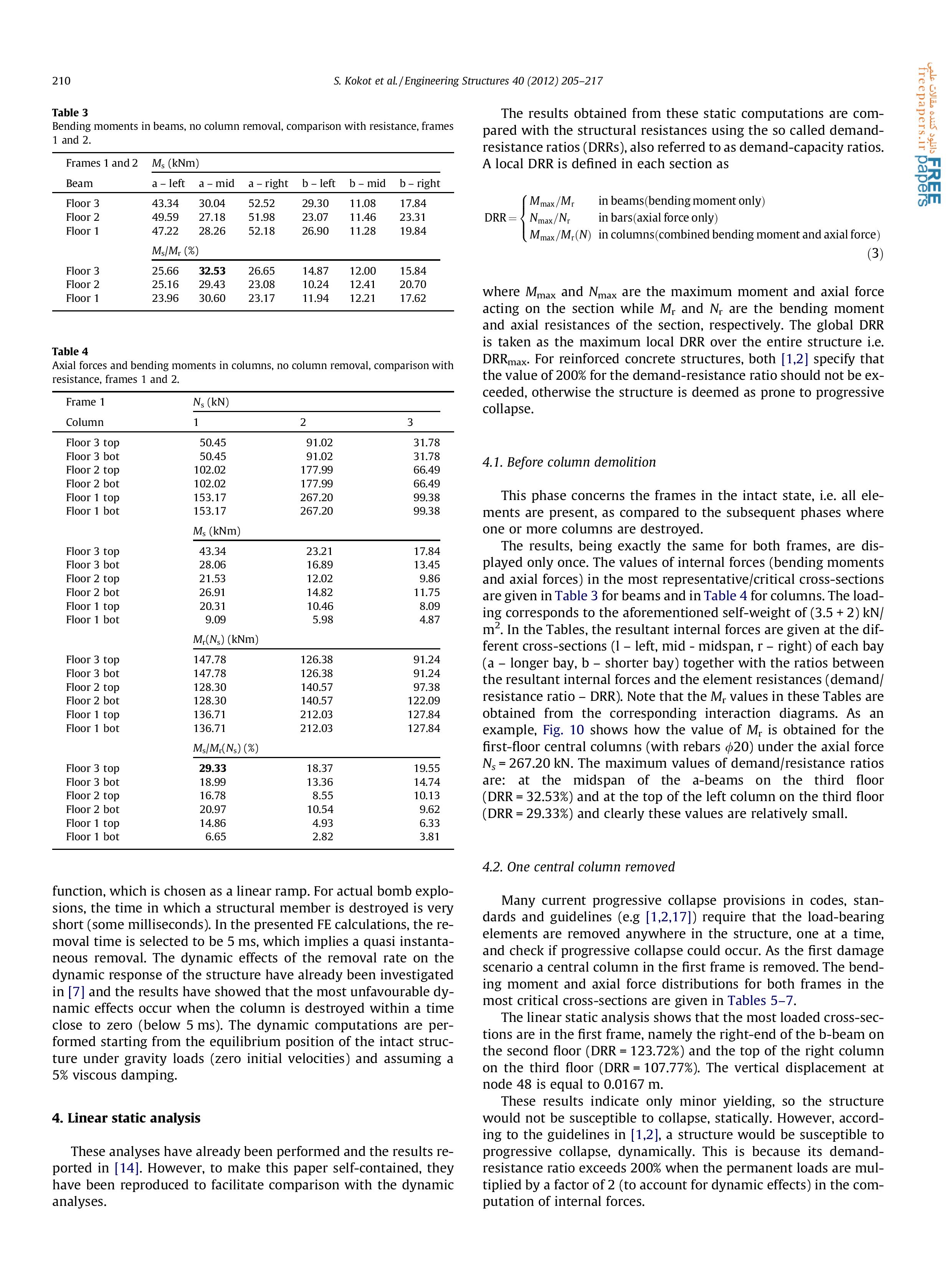
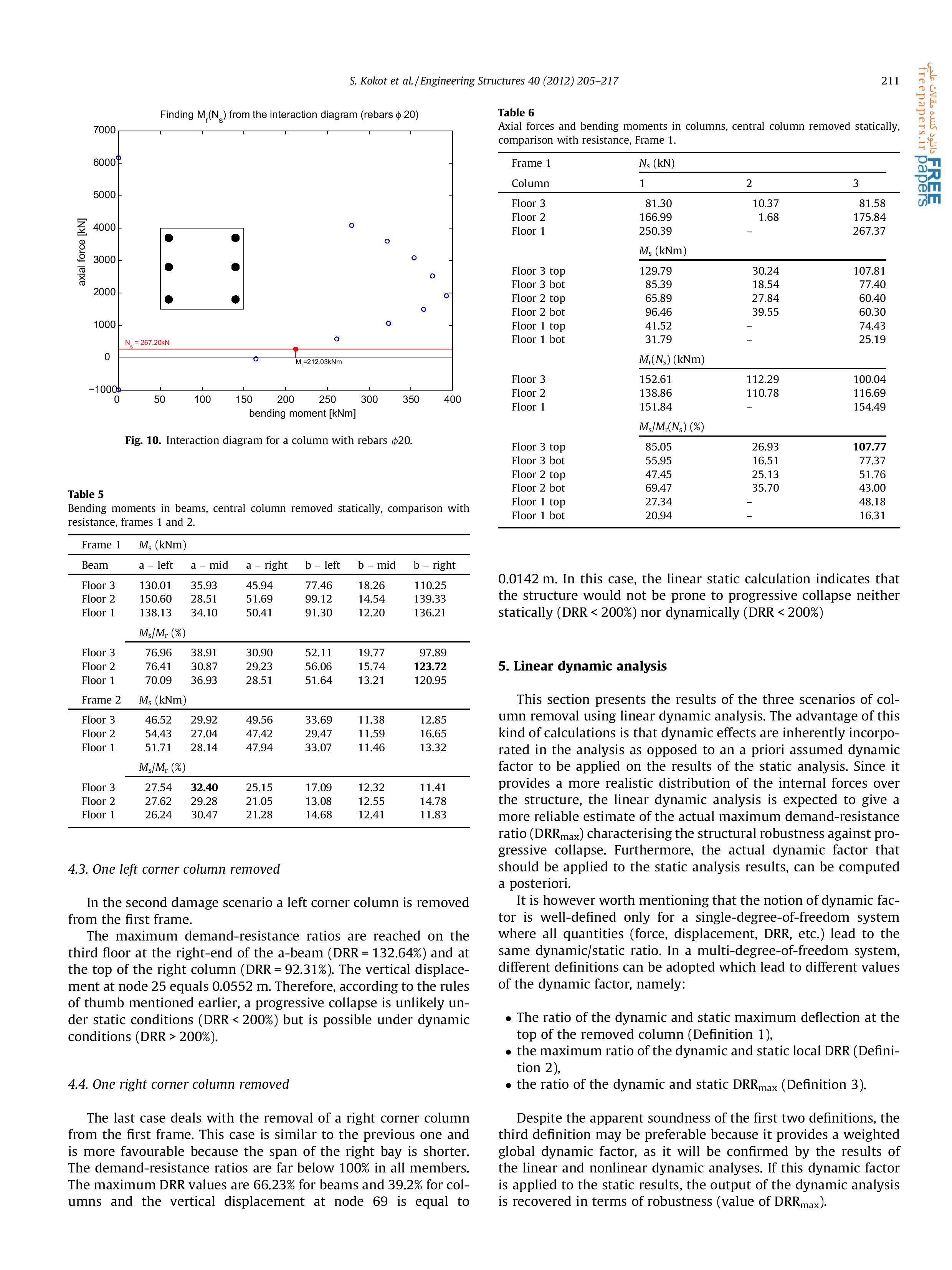
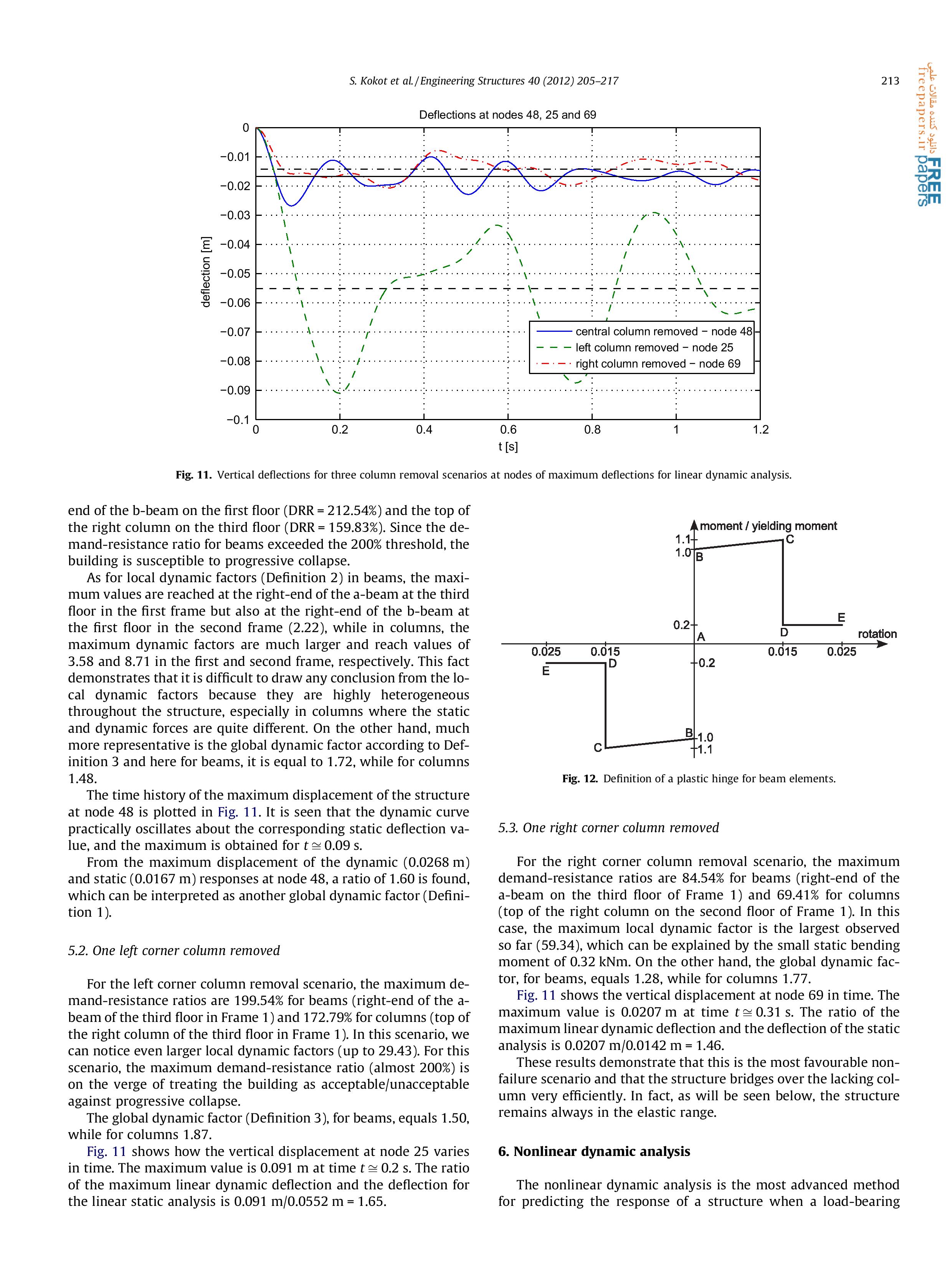
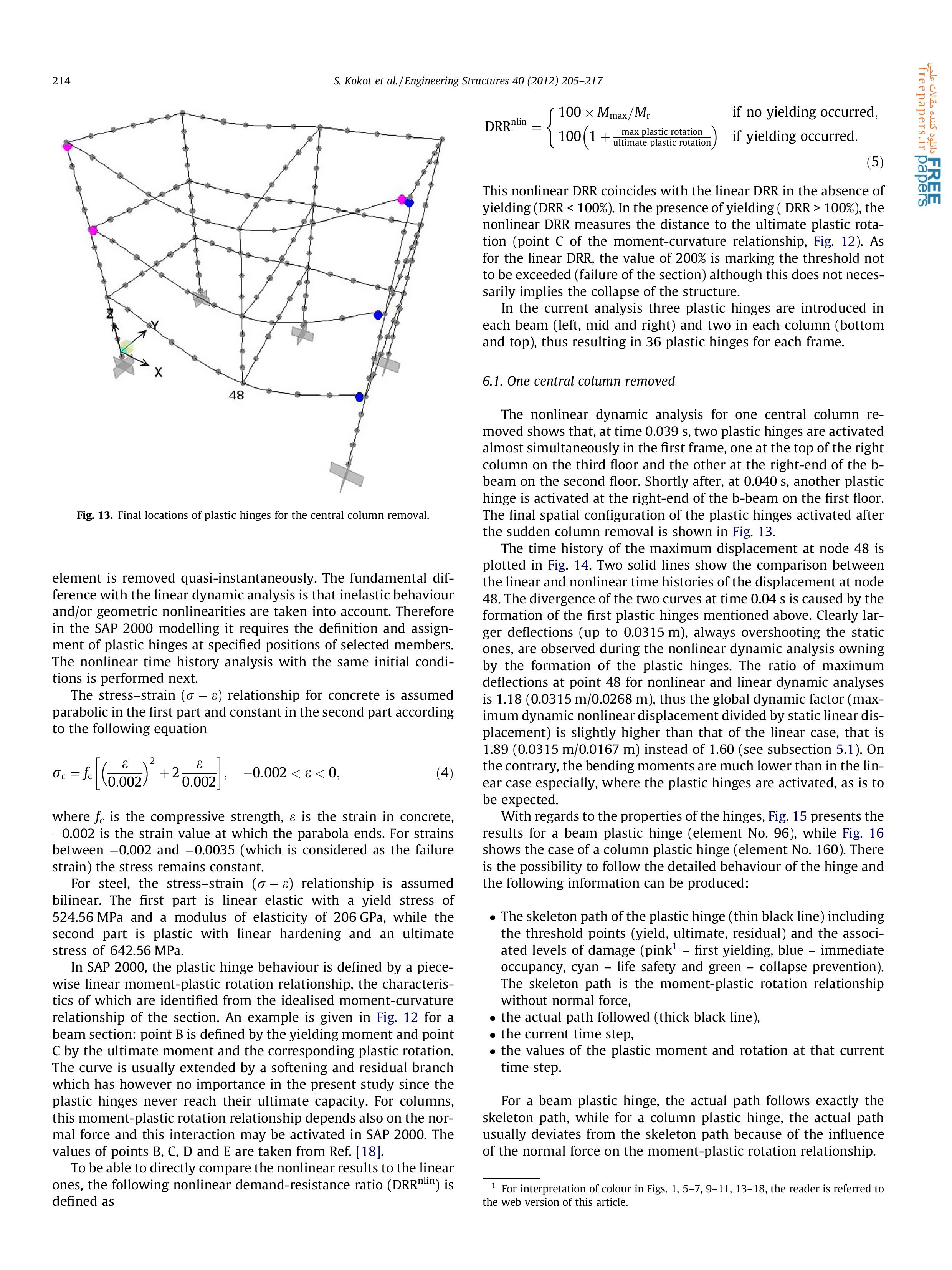
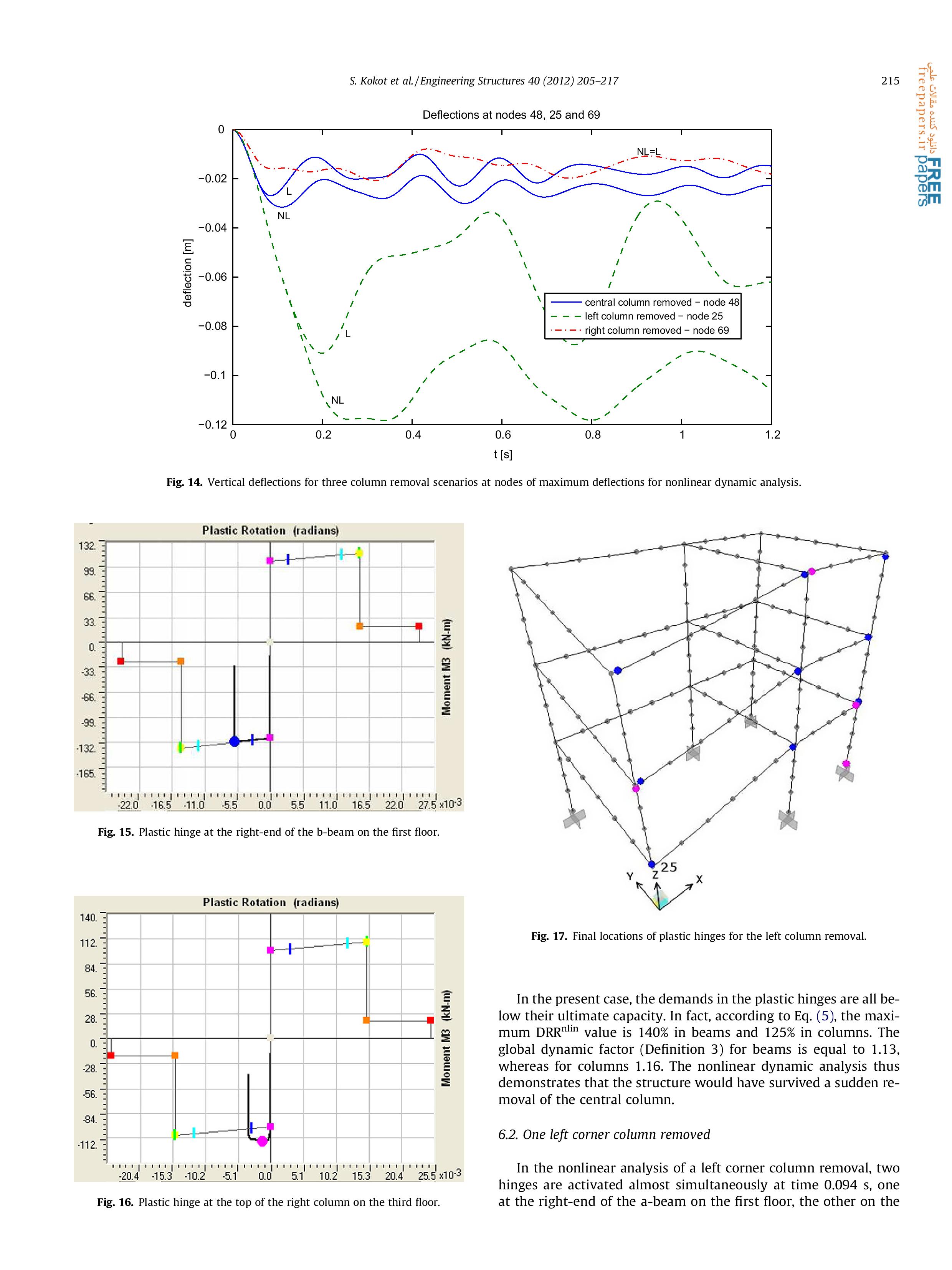
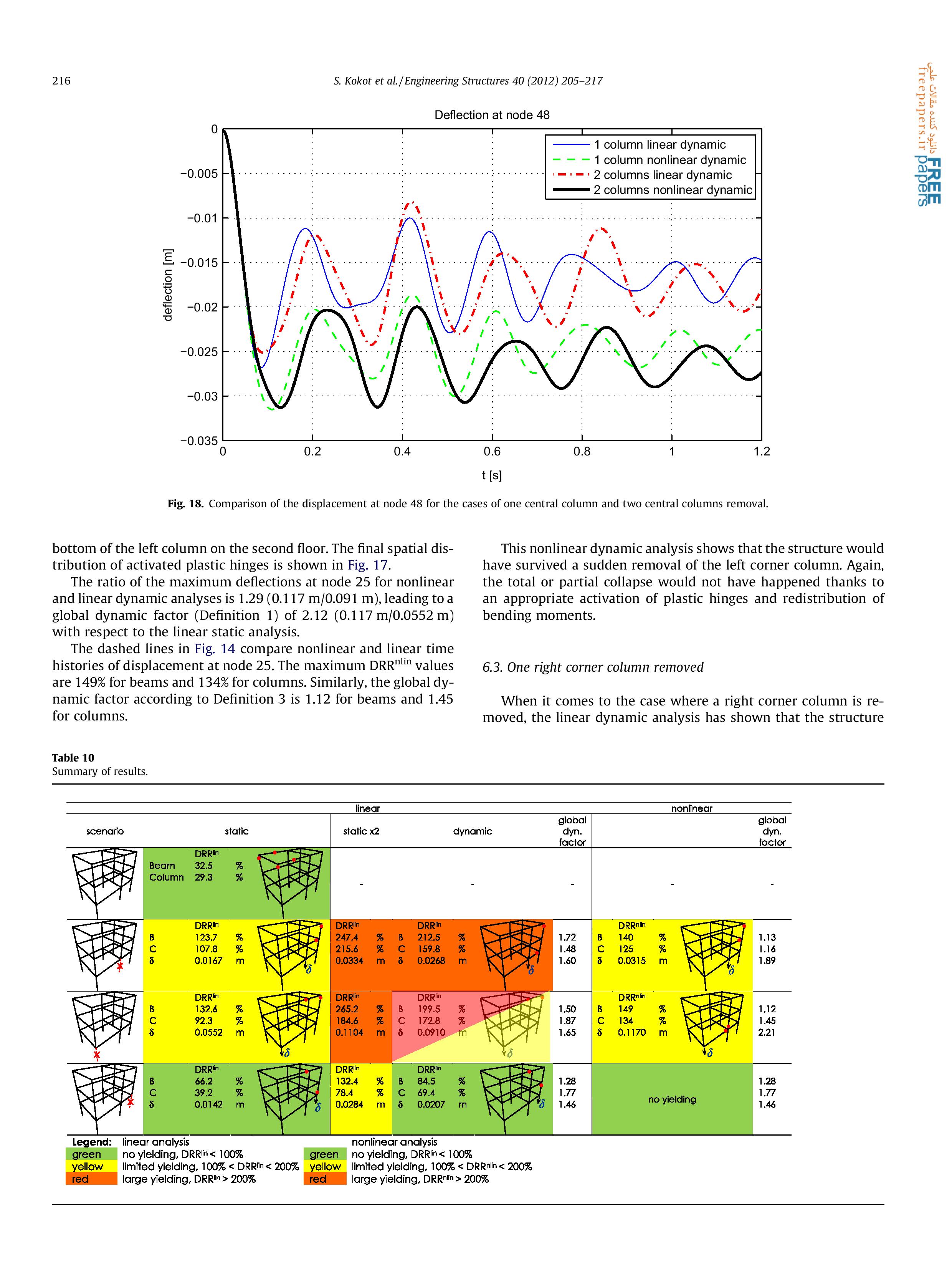
Статья 2. Seweryn Kokot , Armelle Anthoine, Paolo Negro, George Solomos. Static and dynamic analysis of a reinforced concrete flat slab frame building for progressive collapse. Engineering Structures 40 (2012) 205–217.
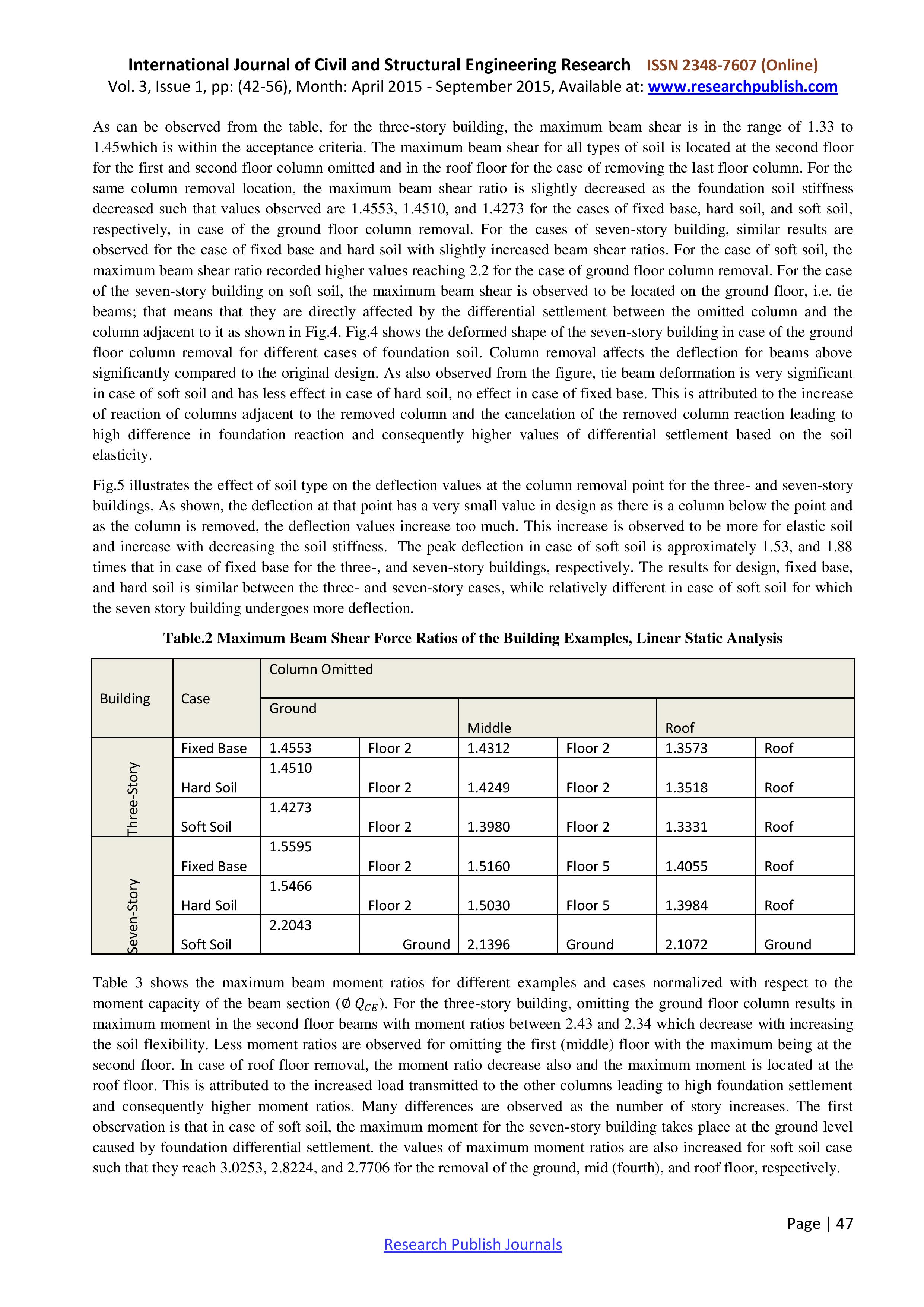
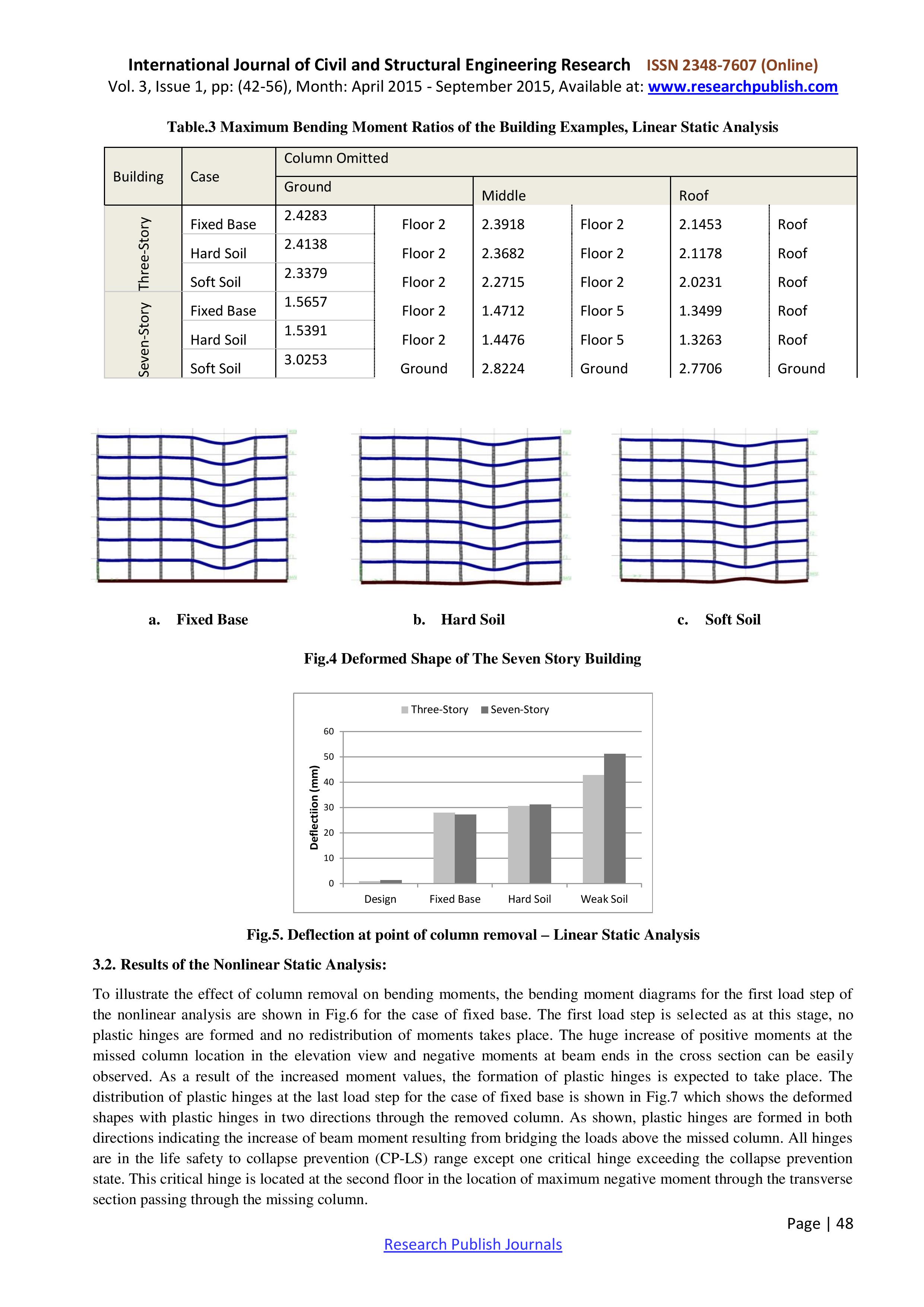
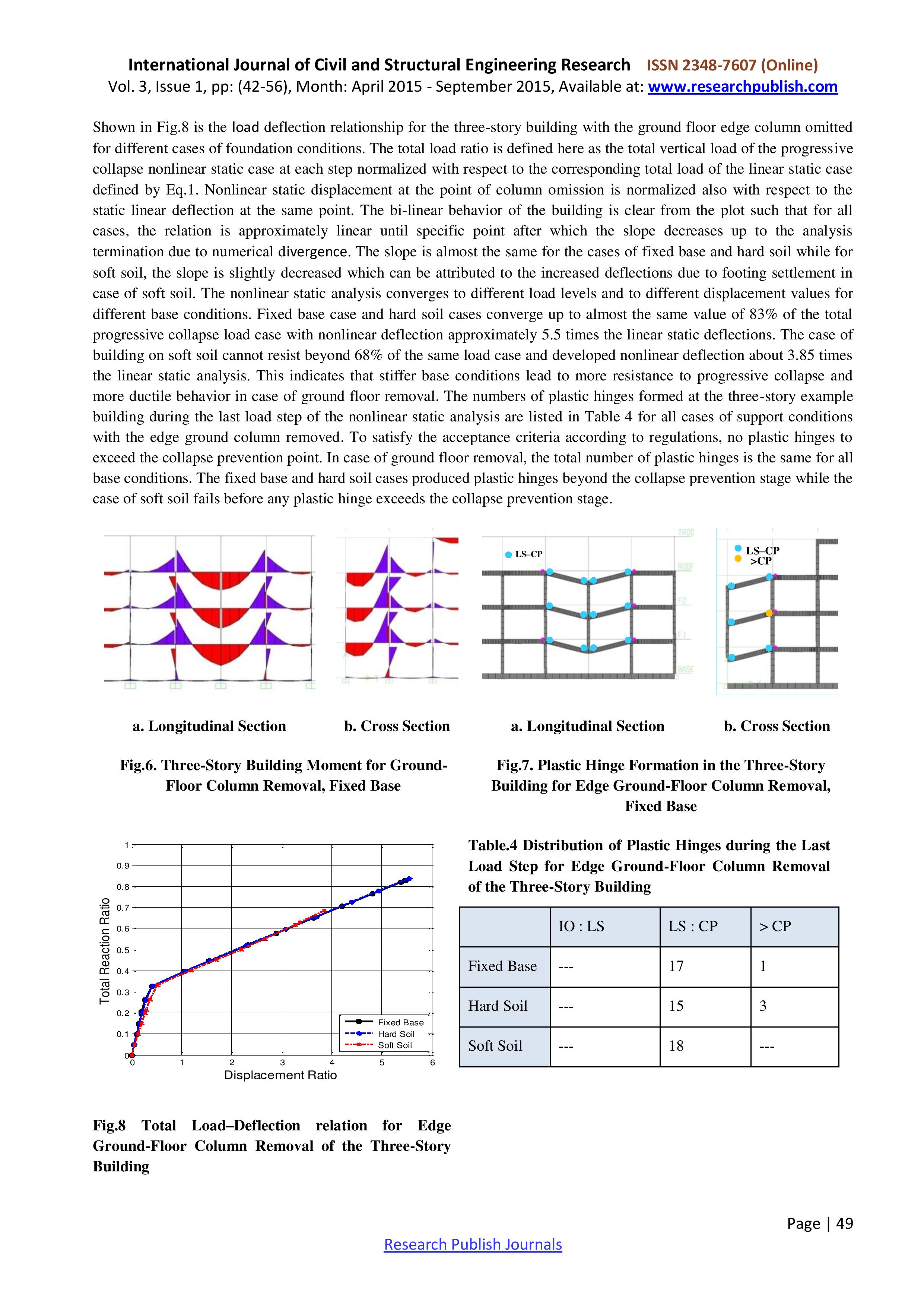
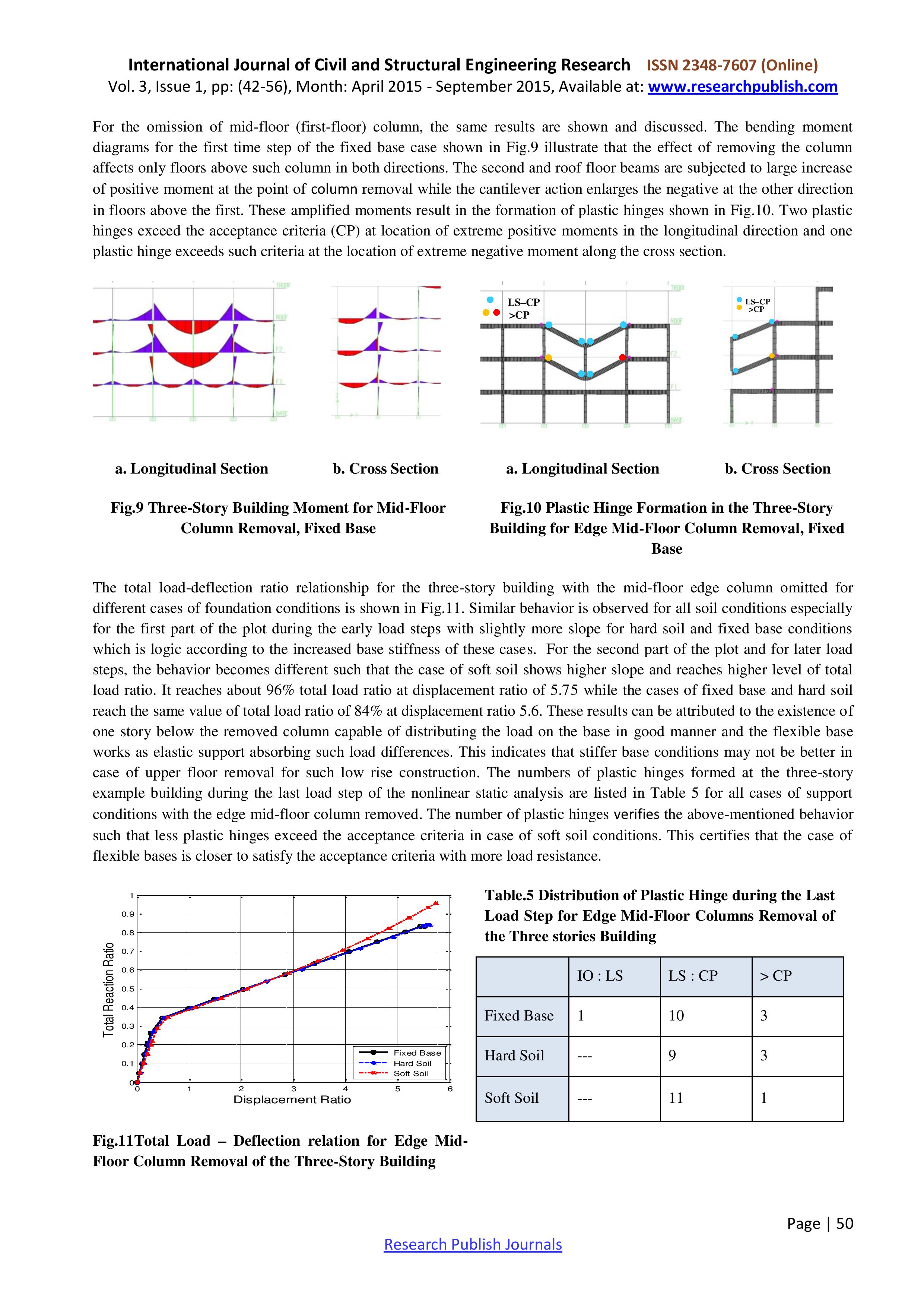
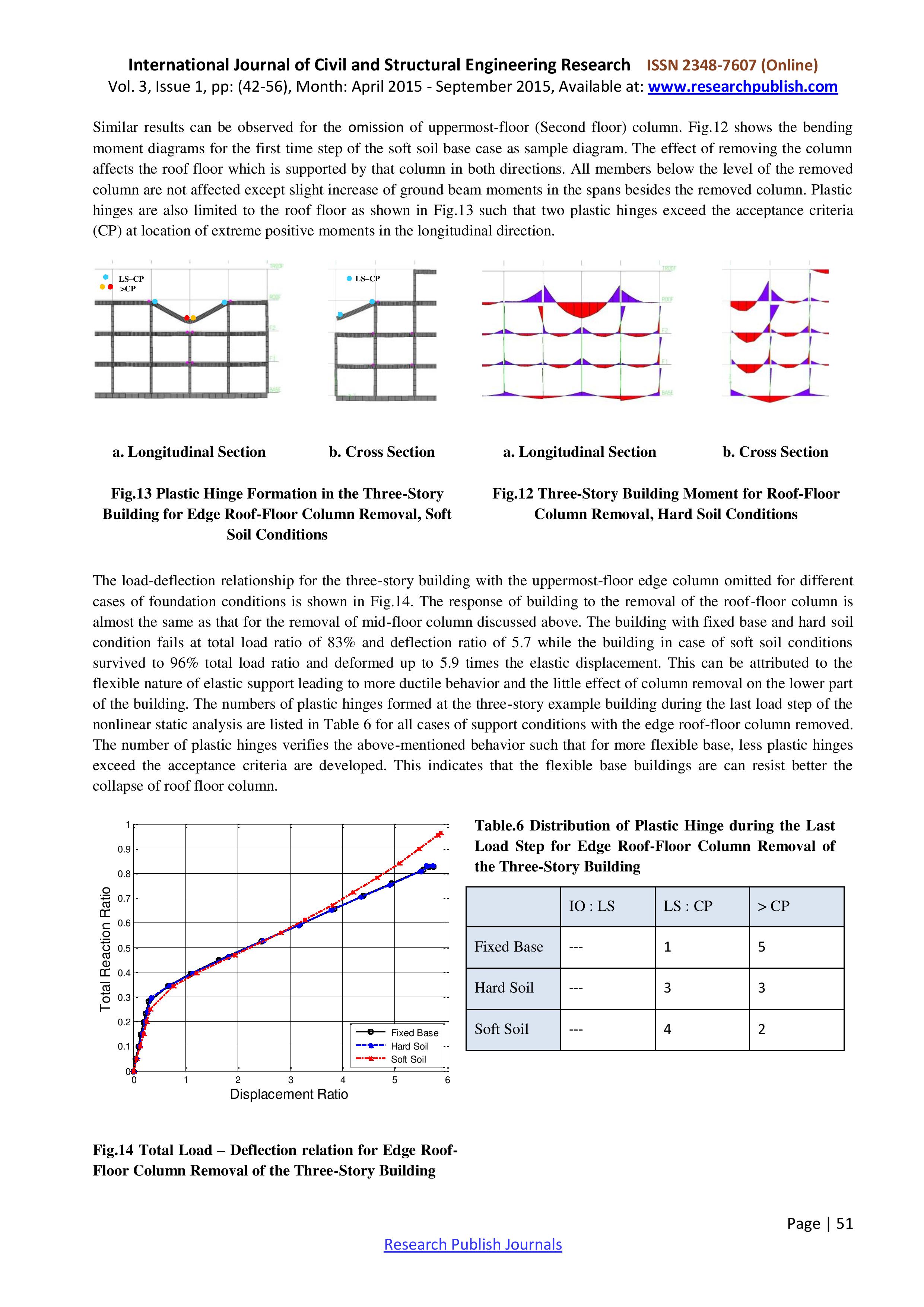
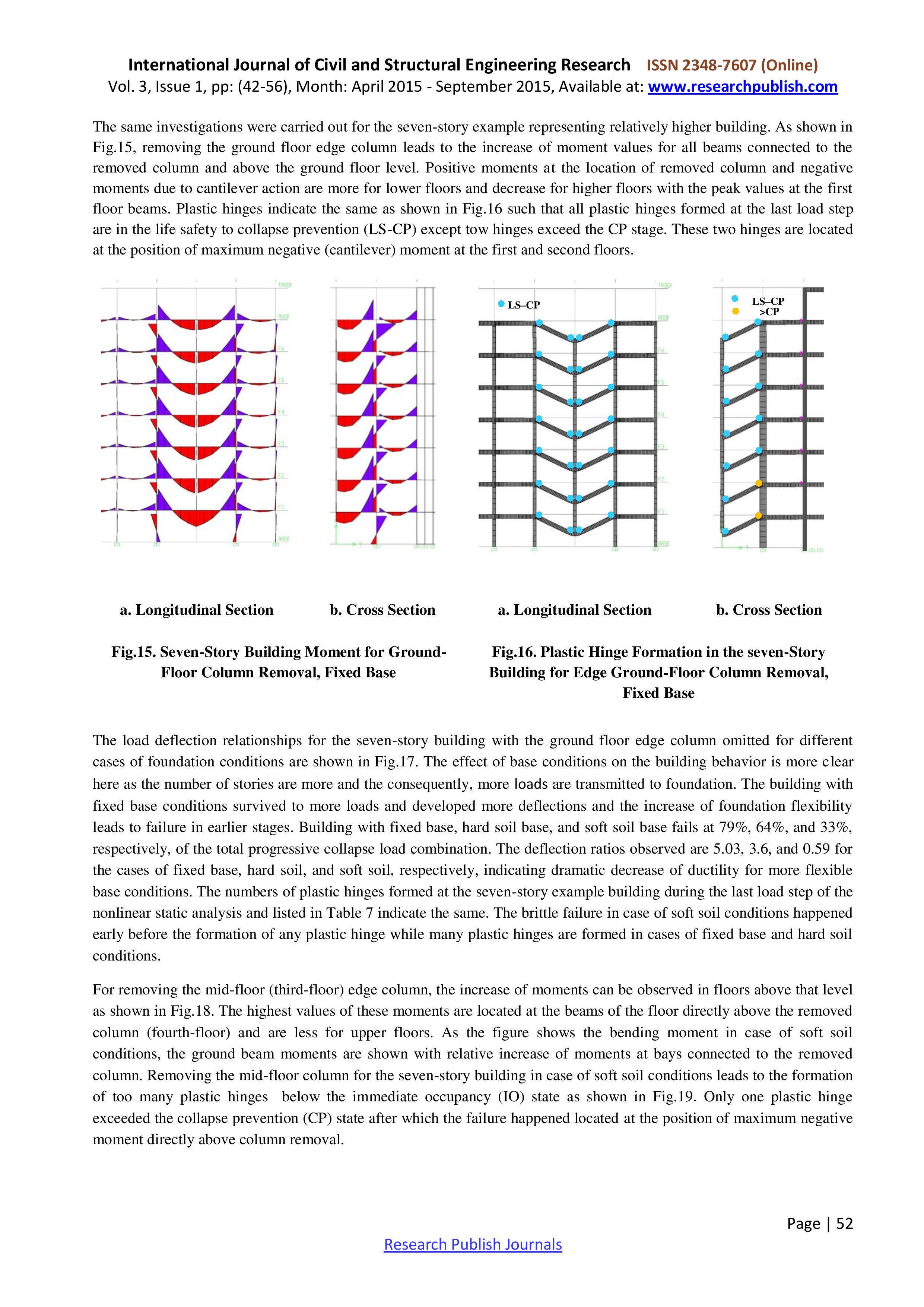
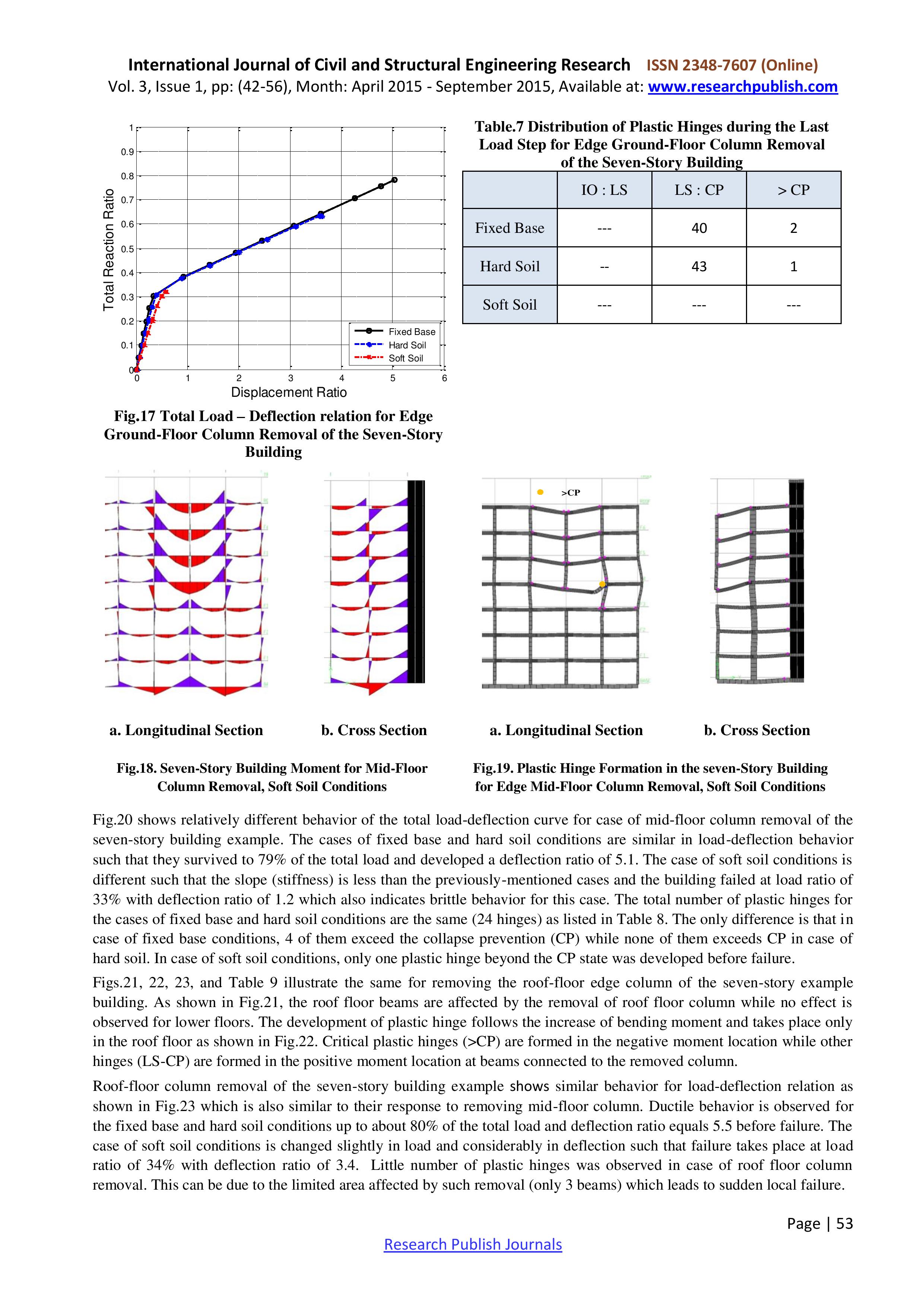
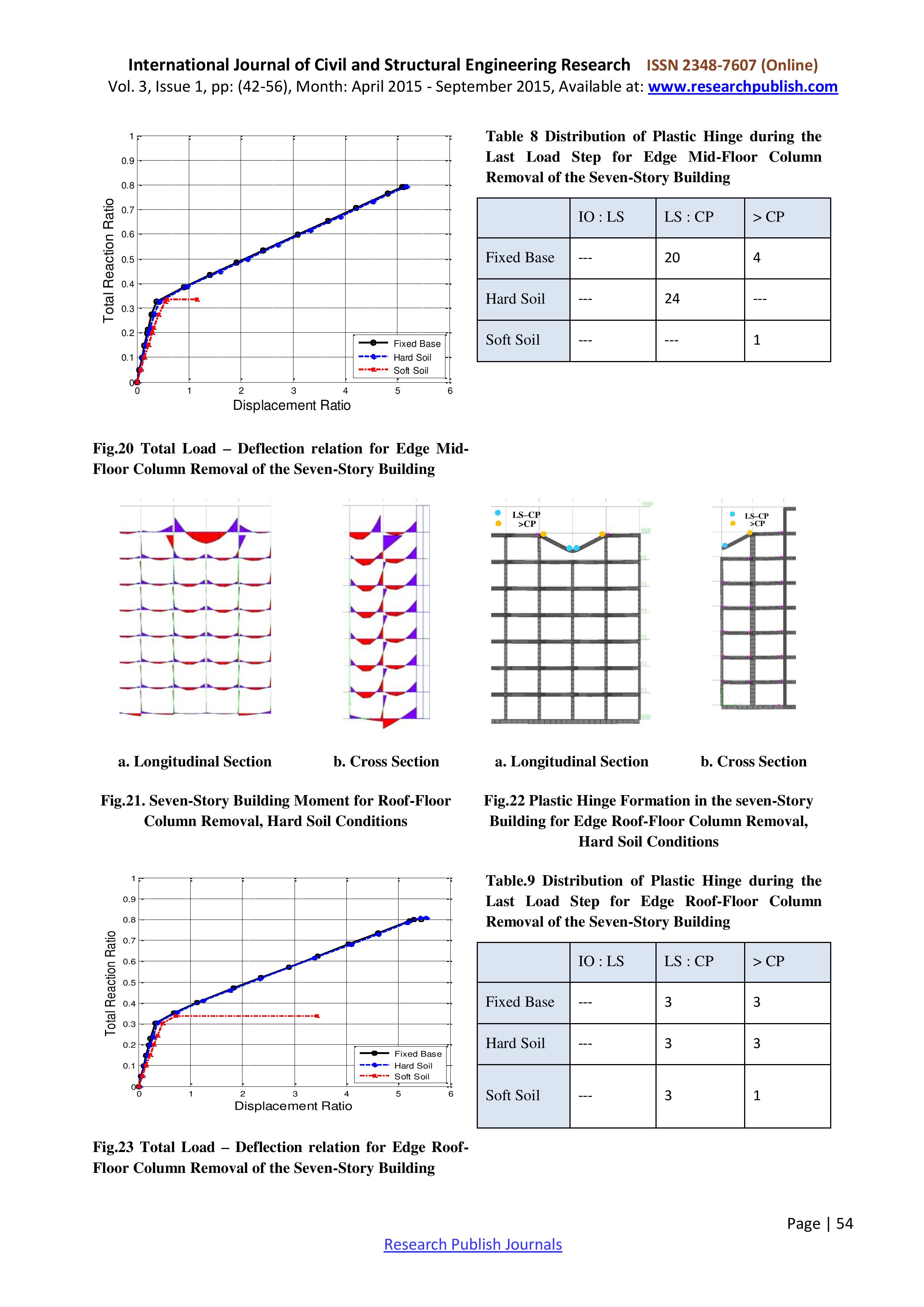
Статья 3. Tharwat A. Sakr Progressive Collapse Analysis of Reinforced Concrete Buildings Including Soil-Structure-Interaction. International Journal of Civil and Structural Engineering Research, Vol. 3, Issue 1, pp: (42-56), Month: April 2015 - September 2015.
Статья 4 B. Santafe Iribarren, P. Berke, Ph. Bouillard, J. Vantomme , T.J. Massart. Investigation of the influence of design and material parameters in the progressive collapse analysis of RC structures. Engineering Structures, vol. 33(10), pp 2805-2820, 2011.
Статья 5. Kuan-Hsoung, Chen Ke-Hung Liao, Yu-Hsiang Chen. Fragility Assessment of Progressive Collapse Buildings. Journal of China University of Science and Technology Vol.48-2011.07.
Статья 6. Bhavik R. Patel. Progressive Collapse Analysis of RC Buildings Using NonLinear Static and Non-Linear Dynamic Method. International Journal of Emerging Technology and Advanced Engineering Website: www.ijetae.com (ISSN 2250-2459, ISO 9001:2008 Certified Journal, Volume 4, Issue 9, September 2014).
Статья 7. Hyunkoo Kang, Madhuri Thimmappa, and Jinkoo Kim. Design of Steel Moment Frames against Collapse. International Conference on Environment And Civil Engineering (ICEACE’2015) April 24-25, 2015 Pattaya (Thailand).
Статья 8. A.U. Qazi, A. Majid, A. Hameed1 and M. Ilyas. Non Linear Progressive Collapse Analysis of RC Frame Structure. Pak. J. Engg. & Appl. Sci. Vol. 16, Jan., 2015 (p. 121–132).
Публикация 9. Hyunjin kim. Dissertation «Progressive Collapse Behavior of Reinforced Concrete Structures with Deficient Details The University of Texas at Austin», August 2006.
Статья 10. H.R. Tavakoli, A. Rashidi Alashti. Evaluation of progressive collapse potential of multi-story moment resisting steel frame buildings under lateral loading. Scientia Iranica A (2013) 20 (1), 77–86
Статья 11. Ashraf Habibullah, S.E.1, and Stephen Pyle, S.E. Practical Three Dimensional Nonlinear Static Pushover Analysis. Structure Magazine, Winter, 1998.


