Учет деформированной схемы при определении усилий для расчета баз колонн и фундаментов

Используемые источники

1. СП 16.13330.2017 Стальные конструкции. Изм. 5.
2. СП 294.1325800.2017 Конструкции стальные. Правила проектирования. Изм. 3.
3. Тимошенко С. П. Сопротивление материалов. Том первый. Элементарная теория и задачи. Перевод В. Н. Федорова с третьего американского издания. Издание второе. Издательство «Наука». Главная редакция физико-математической литературы., М:. 1965 г.
4. Уведомление о разработке проекта свода правил изменение № 5 к СП 16.13330.2017 «СНИП II-23-81* Стальные конструкции». Там скачать документ  СП 16 СО (1).pdf (pdf, 2 MB) Сводка замечаний и предложений к проекту изменения № 5 СП 16.13330.2017 «Стальные конструкции».
5. Уведомление о разработке проекта свода правил изменение № 5 К СП 20.13330.2016 нагрузки и воздействия». Там скачать документ Изм5 к СП 20 (2).pdf (pdf, 1 MB).
6. Мостков М. М. Уточненные решения вопросов устойчивости и изгиба, Государственное издательство Бeлорусcии, 1936 г.
7. СП 63.13330.2018 Бетонные и железобетонные конструкции. Основные положения. Изм. 2.
    

Введение

Речь в первую очередь пойдет об одноэтажных зданиях со стальным каркасом, но может быть распространена и на иные сооружения со схожей работой внецентренно сжатых элементов (колонн).

Согласно п. 7.3.2, 7.3.3 и рис. 3 [2] при проверке устойчивости элемента в плоскости момента используется расчетная схема в виде внецентренно сжатой шарнирной стойки, используются усилия из линейного расчета, при этом через коэффициент φ_e учитывается деформированная схема (геометрическая нелинейность). Учет деформированной схемы увеличивает изг. момент за счет роста прогиба элемента. Фактически проверка устойчивости - это проверка прочности с увеличенным за счет прогиба элемента изг. моментом. Вполне логично учитывать увеличение момента не только при проверке колонны как элемента каркаса, но и при проверке базы и проверке фундамента, т. к. там действует тот же увеличенный момент. Однако, прямые указания в нормативных документах по определению указанного момента отсутствуют.

В строке 46 таблицы документа [4] на предложение о внесении в [1] указаний о необходимости учета деформированной схемы при определении усилий на базу ЦНИИСК им. В.А. Кучеренко дал ответ, что это не требуется, поскольку и так понятно, что надо все учитывать в т. ч. деформированной схему.

Далее предлагается способ определения изг. момента с учетом деформированной схемы.

Рисунок 3 из [2].

Определение момента с учетом деформированной схемы (далее М_деф)

В п. 56, стр. 219 [3] приводится описание и решение расчетной схемы принятой при проверке устойчивости в [1] и описанной выше. Приводимое решение точное (в пределах точности предпосылок исходного дифф. уравнения). Там же имеется описание связи между расчетными схемами в виде внецентренно сжатой консолью и в виде внецентренно сжатой шарнирной стойкой.

 Фрагмент из [3]

Пропуская промежуточные выкладки, см. далее:

 Фрагмент из [3]

Полагая Pe=M₀ и применив более привычные символы:

 , где:

М, М₀ - изг. момент соответственно с учетом деформированной схемы и из линейного расчета, L - расчетная длина принятая для проверки устойчивости элемента, N - продольная сила, E*I - изгибная жесткость.

Сравнение значений М_деф полученных по предлагаемой формуле и полученные нелинейным расчетом в МКЭ-программе

Для сопоставления результатов полученных разными способами взят пример консольной колонны высотой 7 м (L_ef=14 м) из дв. 35Ш1 из стали С255 с усилиями N=300 КН, M=100 КН*м, что примерно соответствует поперечной раме одноэтажного однопролетного здания высотой 7 м, пролетом 21 м, шаг колонн 6 м, в 4  снеговом районе, в 3 ветровом районе.

Расчет по формуле:

Расчет в программе RFEM5:

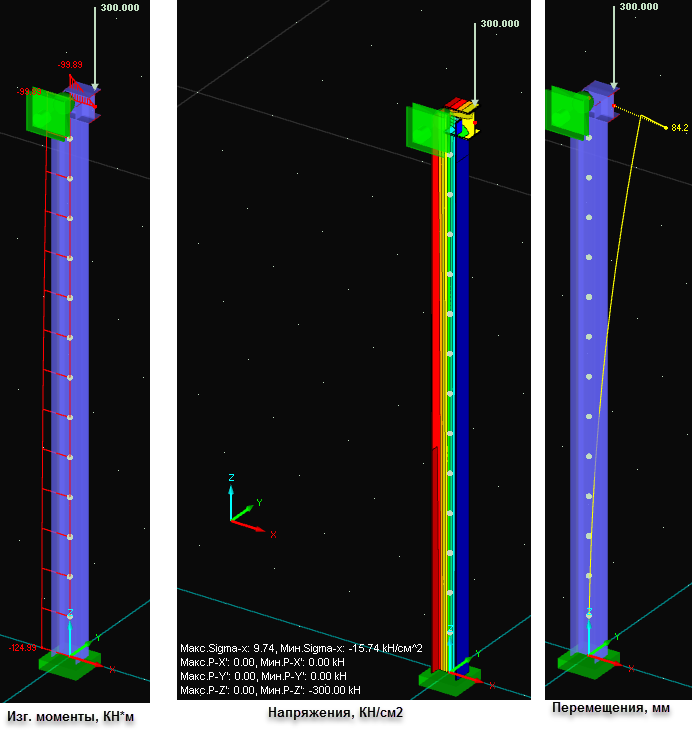
Результаты проверки колонны в программе SCAD Office:

Примечания

1. Приведенный способ учета деформированной схемы предполагает только упругие деформации в сечениях элемента. В реальных колоннах возможны и пластические деформации (см. 4 абз. п. 7.3.2 [2]), это даст несколько бóльшее (порядка 10 %) значение, чем по приведенной формуле. Проверить наличие пласт. деформаций можно проверкой прочности по ф. (106) [1], используя при этом М_деф, выполнение этого условия будет означать отсутствие пластики.
2. Нормы при проверках устойчивости не разделяют внецентренно сжатые и сжато-изгибаемые элементы, везде перечисляя одни за другими, см. п. 9.2.1, 9.2.2, 9.2.4, 9.2.8, 9.3.1 [1], однако, первые находятся в более слабом состоянии, чем вторые при равных усилиях из линейного расчета. (Хотя, по всей видимости, п. 10.3.8 [1] уточняет указанное упрощение). Использование нормами худшего случая для упрощения расчета логично применить и для определения М_деф, а именно, принять расчетную схему в виде внецентренно сжатой стойки. Впрочем, при желании нетрудно уточнить значение М_деф, приняв вместо принятой тут расчетной схемы колонны более близкую к фактической, например, консольная стойка, момент в которой создается боковой равномерно распределенной нагрузкой, точное решение для такой схемы (и других) имеется на стр. 122, ф. (318) [6].
3. Существует иная приближенная формула определения Mдеф получаемая из приводимой точной путем разложения в ряд и удержания первых членов разложения: Mдеф=M₀/(1-N/Ncr). Такая форма применяется в частности в ф. (108), (122) [1] и в ф. (7.6) [7].
4. Приведенный тут способ вычисления Mдеф имеет погрешность в запас надежности в том же смысле, в котором поэлементный расчет на устойчивость принятый в нормах (см. п. 8.1.3 [2]) имеет погрешность в запас надежности относительно нелинейного расчета всего каркаса. Обоснованностью использования нормами такого упрощения для проверки элементов каркаса можно обосновать применение этого же упрощения для определения усилий от этого каркаса.
5. Рост момента при учете деф. схемы по сравнению с линейным расчетом особенно значителен при больших гибкостях колонн (например, когда сечения подобранны прогибам от ветра или по предельной гибкости) и может достигать 40-50 % (по моим оценкам). Принятие [5] смягчит требования к прогибам от ветра (см. cтр. 15 Пункт 3. Графа 3. [5])  и увеличит гибкости колонн, что так же увеличивает важность учета деф. схемы.
6. Кроме влияния на усилия в базах и фундаментах, учет деформированной схемы увеличивает перемещения, что иногда может стать определяющим сечение колонн фактором. Рост перемещений можно вычислить по аналогичной формуле.
7. Способ вычисления Mдеф через коэффициент φ_e в общем случае неверен, поскольку дает необоснованно завышенные значения особенно при загруженностях значительно меньше 1,000. При приближении загруженности к 1,000 указанная погрешность снижается до нуля (если отсутствует пластика). Указанное несоответствие наблюдается и в приводимом примере: напряжения через φ_e 24*0,78=18,72 кН/см2, а фактические 15,74 КН/см2.
8. Практикуемый совместный расчет здания и фундамента не дает возможности учета деформируемой схемы для усилий на фундаменты при линейном расчете.
9. Файлы маткада, скада и рфем использованные в настоящей заметке тут.