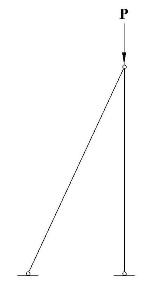
Есть элементарнейшая система из 2-х шарнирных элементов, один из которых вертикален, а другой расположен под некоторым углом, так как показано на рисунке. Внизу оба стержня имеют шарнирно-неподвижные опоры, а в верхней точке системы приложена вертикальная сила. Данная система является неизменяемой и статически определимой: 3К-Ш=3*1-(1+1+1)=0. Составляя уравнения равновесия для верхнего узла, получаем, что усилие в стойке равняется внешней силе, а усилие в подкосе нулевое. Проверяем данный результат по программе – все наши выводы подтверждаются, то есть все верно.
Верно? А как же совместность деформаций и закон Гука? А если угол примыкания подкоса совсем малый, все равно ноль? Так будет или нет усилие в подкосе? Если будет, то… читай заголовок, если не будет, то почему?



Комментарии
Авторизоваться
Ответ: нет, не будет. Иначе, при отбрасывании связи в виде раскоса и заменой ее на реакцию получаем пропеллериз вертикального стержня и шарнира с действующей поперечной силой (горизонтальная составляющая реакции). Грубо говоря, отбрасываем раскос, заменяем его на реакцию и составляем уравнение моментов относительно шарнра в нижнем узле вертикального стержня. Момент в шарнире равен нулю. Следовательно, поперечная сила в верхнем узле равна 0.
2. Раз усилие в наклонном стержне = 0 - то и деформации равно 0.
3. Наклонный стержень остается неизменной длины, вертикальный укорачивается в соответствии с законом Гука. Чертим 2 окружности вокруг "нижних" шарниров обоих стержней и получаем 3-ю точку - "новое" положение верхнего шарнира после всех передряг.
Вывод: строймех дядька Теличко читал не зря на 4 курсе (или на третьем начался строймех? не помню, блин...), не лженаука :D. Усилия в подкосе - 0, совместность перемещений вполне обеспечена.
Только не пинайте сильно бедного КМДшника, который влез за каким-то чертом в спор гуру расчетов :D
Нет, не лже. Вопрос провокационный и поставлен не корректно, вы сначала говорите о том что система статически определима, а потом намекаете на деформированную схему, решение которой не есть статически определимым.
В стротельной механике есть инструменты для решения обеих идеализированных схем (деформированной и не деформированной), результаты будут различны, но в обеих, идеализированных схемах они будут верны.
"Важно, чтобы инженер всегда понимал, что, осуществляя построение модели, он идеализирует конструкцию и всегда должен оценивать адекватность этой идеализации" (с) А.С. Городецкий, И.Д. Евзеров Компьютерные модели конструкций.
С большим к вам уважением.
Не нужно путать условия определения СТЕПЕНИ статической определимости N=3*K-Ш и условие геометрической неизменяемости стержневой системы S=2K-3 (или Sобщ=2K).
Э-э-э, формула n=3*K-Ш дает и то и это :). Если одну из опор предложенной системы сделать подвижной, то n=3*1-4=-1.Четверка здесь потому, что шарнирно-подвижная опора эквивалентна 2-м простым шарнирам, а "-1" означает, что система изменяемая и ей "для полноты счастья" не хватает 1-й связи (в широком смысле),
Про это несколько лет назад была довольно большая тема - поищите.
И к Вам есть вопрос, если позволите - в ЛС. Или тему в профильном разделе форума забацать... Так ведь заклюют же, коршуны))))
Валяйте :)
3-х шарнирная арка принципиально другая конструкция, работающая в общем случае как сжато-изогнутый элемент.
Хорошо, немного не так выразился. Давайте говорить о двух дисках - стержнях, прикрепленных к земле и соединенных между собой шарнирами (каждый из которых в свою очередь можно представить в виде двух стержней, оси которых пересекаются в точке установки шарнира/опоры).
Для трехшарнирной арки условие неизменяемости (которым пользуюсь я N=3*K-Ш)
Не нужно путать условия определения СТЕПЕНИ статической определимости N=3*K-Ш и условие геометрической неизменяемости стержневой системы S=2K-3 (или Sобщ=2K).
Я лишь указал на причину, по которой для СТАТИЧЕСКИ ОПРЕДЕЛИМОЙ конструкции (в этом мы с Вами не спорим) необходимо составлять ДОПОЛНИТЕЛЬНОЕ уравнение, позволяющее раскрыть эту самую статическую определимость. Причиной составления доп. уравнения является то, что условием геометрической неизменяемости системы дисков будет являться способ их соединения с землей - это две шарнирно-неподвижных опоры. И 4 реакции, которые можно найти, НЕ прибегая к рассмотрению совместных деформаций системы.
Вот и покажите!
Постараюсь на след. неделе чего-нибудь сваять... А Вы покритикуете :-)))
ЗЫ У меня заморочка сейчас небольшая, не могу уделить внимание в полной мере... И к Вам есть вопрос, если позволите - в ЛС. Или тему в профильном разделе форума забацать... Так ведь заклюют же, коршуны))))
"Кроме трех уравнений равновесия, которые дает статика для системы сил, расположенных в одной плоскости, для расчета трехшарнирной арки можно ... ".
Прервал цитирование, так как 3-х шарнирная арка принципиально другая конструкция, работающая в общем случае как сжато-изогнутый элемент. В исходной задаче приведена система, имеющая НДС только в виде продольных сил.
С этим четвертым уравнением также связано то, что для трехшарнирной арки не выполняется условие статической неизменяемости S=2K-3. S=2 (2 стержня). K=3 (3 узла). S=2 2K-3=3. Казалось бы, что система изменяемая. Ан нет, условия закрепления арки делают систему неизменяемой. Но одновременно уравнений статики становится недостаточно.
Для трехшарнирной арки условие неизменяемости (которым пользуюсь я N=3*K-Ш) однозначно говорит о том, что система неизменяемая и статически определимая. Она прекрасно решается путем рассечения по центральному шарниру.
Ни о каких величинах "пренебрежимо малых" речи не идет. Если мы остаемся в рамках положения о малости перемещений, то в данной задаче усилие в раскосе будет НУЛЕВОЕ. 0.00000000000
Отнюдь :)
А по поводу численного решения задачи и нахождения величины МАЛЫХ перемещений - в данном случае оно очень простое: это задача о нахождении точки пересечения двух окружностей: одной с радиусом равным длине подкоса, со второй, равной длине стойки минус деформация от продольной силы в этой самой стойке. Составляется и решается квадратное уравнение. Делов-то. И никакого МКЭ тут не нужно. Для любой конфигурации трехшарнирной рамы - можно получить точное решение аналитически.
Вот и покажите!
Цитата:Сообщение #70 от qwerВеличество строймех предлагает не 3, а 4 уравнения равновесия. Строймех рулит)))))
Такой - точно нет :(
Рулит, рулит:-)
По поводу четвертого уравнения - см. стр. 74 Даркова, Шапошникова:
"Кроме трех уравнений равновесия, которые дает статика для системы сил, расположенных в одной плоскости, для расчета трехшарнирной арки можно составить четвертое уравнение, основанное на том, что равнодействующая всех сил, приложенных к левой/правой частям арки, должна пройти через средний шарнир, так как в противном случае левая (или правая) половина арки вращалась бы вокруг точки с".
С этим четвертым уравнением также связано то, что для трехшарнирной арки не выполняется условие статической неизменяемости S=2K-3. S=2 (2 стержня). K=3 (3 узла). S=2 2K-3=3. Казалось бы, что система изменяемая. Ан нет, условия закрепления арки делают систему неизменяемой. Но одновременно уравнений статики становится недостаточно. А так как система статически определима, откуда-то четвертое уравнение нужно вытащить. Вот и вытаскивается оно - см. цитату выше.
А таки да - основа основ - это гипотеза малости перемещений. Если условно положить вертикальную стойку, сделанную из пластилина, а подкос - большой жесткости - применять стандартные уравнения нельзя.
усилия в раскосе будут, но (при малых перемещениях) пренебрежимо малые
. Ни о каких величинах "пренебрежимо малых" речи не идет. Если мы остаемся в рамках положения о малости перемещений, то в данной задаче усилие в раскосе будет НУЛЕВОЕ. 0.00000000000
А по поводу численного решения задачи и нахождения величины МАЛЫХ перемещений - в данном случае оно очень простое: это задача о нахождении точки пересечения двух окружностей: одной с радиусом равным длине подкоса, со второй, равной длине стойки минус деформация от продольной силы в этой самой стойке. Составляется и решается квадратное уравнение. Делов-то. И никакого МКЭ тут не нужно. Для любой конфигурации трехшарнирной рамы - можно получить точное решение аналитически.
Величество строймех предлагает не 3, а 4 уравнения равновесия. Строймех рулит)))))
Такой - точно нет :(
В общем верный ответ дан: усилия в раскосе будут, но (при малых перемещениях, которые являются одной из гипотез/условий применения строймеха и сопромата) пренебрежимо малые. Для закрытия темы в ближайшее время дам свое решение.
Но я смотрю разобрались всё-таки.
Такие системы надо считать по "Деформированной схеме".
+5 за задачку!
Для нахождения всех опорных реакций его Величество строймех предлагает не 3, а 4 уравнения равновесия. Четвертое уравнение - момент равнодействующей всех сил относительно замкового шарнира, слева или справа.
Из этих четырех уравнений прекрасно определяются все опорные реакции. Которые для левой половины будут нулевыми (вследствие прохождения внешней нагрузки по линии, соединяющей правую опору и замковый шарнир).
Следовательно, будет равно нулю и усилие в подкосе. Даже, если угол примыкания очень мал. Все зависит от направления силы P.
Никакого нарушения условий совместности деформаций здесь нет, равно как и нарушения закона Гука.
Строймех рулит)))))
Хотелось бы математики, что ли ...
Извольте: http://1drv.ms/1G404FQ
Разрешающая система уравнений содержит трансцендентные функции и была решена в Экселе с помощью надстройки "Поиск решения".
Вывод. Деформация подкоса в десять тысяч раз меньше, чем у стойки, подкос практически не деформируется.