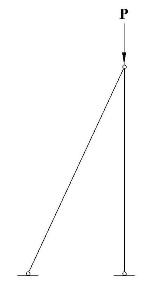
Есть элементарнейшая система из 2-х шарнирных элементов, один из которых вертикален, а другой расположен под некоторым углом, так как показано на рисунке. Внизу оба стержня имеют шарнирно-неподвижные опоры, а в верхней точке системы приложена вертикальная сила. Данная система является неизменяемой и статически определимой: 3К-Ш=3*1-(1+1+1)=0. Составляя уравнения равновесия для верхнего узла, получаем, что усилие в стойке равняется внешней силе, а усилие в подкосе нулевое. Проверяем данный результат по программе – все наши выводы подтверждаются, то есть все верно.
Верно? А как же совместность деформаций и закон Гука? А если угол примыкания подкоса совсем малый, все равно ноль? Так будет или нет усилие в подкосе? Если будет, то… читай заголовок, если не будет, то почему?



Комментарии
Авторизоваться
Раз жесткость подкоса совсем не важна, предлагаю его заменить бесконечно жестким шарнирным стержнем. Тем самым преобразовав треугольник в шарнирную стойку. Можем так поступить?
Как классно, оппоненты сами подкидывают аргументы о ... э-э-э ... лженаучности. Казалось бы да, можно заменить, но тогда горизонтального перемещения не будет вовсе. Соответственно раскос получит только вертикальное перемещение и, соответственно, будет сжат :).
Так у Вас есть ответы на Ваши же вопросы? Чего же Вы мучаете публику, покажите всем что строймех - лженаука. Ну или наоборот - наука.
Не-а, не покажу, по крайней мере пока. Считаю, что "публика" должна сама разобраться с этим (элементарным!?) вопросом о научности/корректности основополагающей строительной науки. О чем, собственно, и написал в аннотации :). Правда все, кроме Вас, чегой-то давно слиняли :).
Так что пока нагло заявляю ... см. заголовок :)
Будем считать это подсказкой №1 :)
Так у Вас есть ответы на Ваши же вопросы? Чего же Вы мучаете публику, покажите всем что строймех - лженаука. Ну или наоборот - наука.
Смею утверждать, что жесткость подкоса при линейной постановке задачи не имеет вообще никакого значения.
А чего Вы оговариваетсь о линейной постановке задачи? Я же ответил, что при линейном расчете подкос всегда будет нулевым как по усилиям, так и деформациям. При этом будет выполняться и закон Гука и совместность деформаций. Даже привел подобие кинематического анализа полученного механизма.
Раз уж Ваш вопрос такой однозначный, то прошу однозначно ответить на вопрос: какой расчет правильный - линейный или нелинейный?
Для однозначного ответа на этот вопрос не хватает исходных данных к смысловой нагрузке. Какова жесткость подкоса?
Смею утверждать, что жесткость подкоса при линейной постановке задачи не имеет вообще никакого значения. Всяческие бесконечности и нули оставим за скобками. Будем считать это подсказкой №1 :)
Вот так, вынужден подсказывать, а то исходный тезис так и останется не
опровергнутым.
А знаете, подсказывать не буду. Буду наоборот спорить до тех пор, пока кто-нибудь не докажет несостоятельность исходного вывода :))
Вопрос стоит однозначно: будет или нет деформации (усилия) в подкосе
Для однозначного ответа на этот вопрос не хватает исходных данных к смысловой нагрузке. Какова жесткость подкоса? При бесконечной жесткости деформации будут нулевыми при конечном значении усилия. При конечной жесткости будет конечное значения деформации при конечном значении усилия. Допустим значение усилия в подкосе = 0. Это конечное или бесконечное значение? Если конечное, то подкос, какую конечную жесткость ему не назначь при нулевом усилии можно считать бесконечно жестким. Вот он и весь дуализм Вашей схемы.
Ну , от чего-то же нужно оттолкнуться для доказательства или опровержения существования совместности деформаций и перемещений для данной системы при выполнениии закона Гука?
Вопрос стоит однозначно: будет или нет деформации (усилия) в подкосе и насколько строительная механика адекватна в этом вопросе. Пока говорим только о линейном расчете без всяких там деформационных моделей. А оттолкнуться надо, видимо, от определения в общем виде деформаций по осям, теоремы Пифагора и ... ну ... и чего-нибудь еще, что покажет, что при любых смещениях верхней точки длина раскоса остается неизменной.
Ага, вот и Вы уже начинаете склоняться к "мутности" сей дисциплины :)).
Ну давайте тогда называть и математику мутной лженаукой, т.к. она содержит неопределенности типа 0/0, ∞/∞, 0/∞.
Увы, сей аргумент за "неадекватов" (вроде IBZ) принять не могу - нет тут никакого дуализма, а есть геометрически неизменяемая статически определимая система без намека на мгновенную изменяемость.
Тогда откуда сомнения в верности решения?
Там не верна посылка о НЕИЗМЕННОЙ ДЛИНЕ ПОДКОСА. Именно "сомнение" в верности этого и высказано в исходном тексте. Там, правда, говорится об усилии, но это вещи напрямую связанные. Вы же считаете неизменность длины аксиомой и именно на этом строите всю систему доказательств, не очень, правда, понятно чего именно.
Нет, не так. Неизменной длину подкоса мы принимаем(а не утверждем ее аксиомой), из Вашей непоколебимой уверенности в том, что данная система "есть геометрически неизменяемая статически определимая система без намека на мгновенную изменяемость". Ну , от чего-то же нужно оттолкнуться для доказательства или опровержения существования совместности деформаций и перемещений для данной системы при выполнениии закона Гука? Как можно доказывать, что
...ДЛИНА ПОДКОСА в результате вертикального и горизонтального смещений (они оба, действительно, будут присутствовать) верхней точки НЕ ИЗМЕНИЛАСЬ
посылки о НЕИЗМЕННОЙ ДЛИНЕ ПОДКОСА
Вообще-то один из Ваших вопросов в шапке звучит так
Я отвечаю - да, верно, и показываю аналитически одновременную совместность перемещений, деформаций и выполнение закона Гука. Что не так? А не так лишь только то, что образованный смещениями общего узла, из этого вобщем-то правильного вывода, под нагрузкой треугольник не может находится в равновесии даже при выполнении условия совместности деформаций и выполнения закона Гука. Но это же совсем другой вопрос:)))
Конечно, строго говоря Ваш треугольник не МИС, но при этом обладает свойствами МИС.
Ага, вот и Вы уже начинаете склоняться к "мутности" сей дисциплины :)). Увы, сей аргумент за "неадекватов" (вроде IBZ) принять не могу - нет тут никакого дуализма, а есть геометрически неизменяемая статически определимая система без намека на мгновенную изменяемость.
Я же выводил в общем виде совместность перемещений и углов поворота при неизменной длине подкоса. Что там не верно?
Там не верна посылка о НЕИЗМЕННОЙ ДЛИНЕ ПОДКОСА. Именно "сомнение" в верности этого и высказано в исходном тексте. Там, правда, говорится об усилии, но это вещи напрямую связанные. Вы же считаете неизменность длины аксиомой и именно на этом строите всю систему доказательств, не очень, правда, понятно чего именно.
Признаком же мгновенной изменяемости является временное (до перемещений) совпадение векторов возможных перемещений в точке соединения элементов.
Еще одним признаком мгновенной изменяемости является то, что верный расчет такой системы можно выполнить только с учетом изменений ее геометрии от конечных перемещений. Конечно, строго говоря Ваш треугольник не МИС, но при этом обладает свойствами МИС.
Очень даже может быть, но доказательств в общем виде пока нет :(. А всего то и надо показать в общем виде, что длина подкоса в результате вертикального и горизонтального смещений (они оба, действительно, будут присутствовать) верхней точки не изменилось...
Я же выводил в общем виде совместность перемещений и углов поворота при неизменной длине подкоса. Что там не верно?
А может узел останется единым, а вот деформируется только один элемент?:)
Очень даже может быть, но доказательств в общем виде пока нет :(. А всего то и надо показать в общем виде, что длина подкоса в результате вертикального и горизонтального смещений (они оба, действительно, будут присутствовать) верхней точки не изменилась... А иначе - смотри заголовок :))
Ваша формула 3К-Ш
Не-а, не моя, "это было до вас в 17-м веке"(с) :)
Чем дальше, тем меньше я понимаю благородного дона :) В МКЭ программе я могу увидеть только конечные перемещения, направления же векторов ВОЗМОЖНЫХ перемещений анализируются ДО НАГРУЗОЧНЫХ ДЕФОРМАЦИЙ.
Все верно, благородный дон слегка утомился и не о том подумал.
P.S.Вообще то изменяемость, в том числе и мгновенная, анализируется по всем возможным направлениям во вне зависимости от конкретной нагрузки.
МИС, по определению, не является геометрически изменяемой системой. МИС при малых перемещениях ведет себя как механизм.
А может узел останется единым, а вот деформируются оба элемента?:)
А может узел останется единым, а вот деформируется только один элемент?:)
Да где уж мне, я вот один треугольник осилить не могу, а тута их аж два :)), да и формулы никакой я не знаю :(
Ну как это? Ваша формула 3К-Ш. А треугольников хоть и два - "проблема" та же что и у Вашего.
Именно сей факт Вы сможете понаблюдать анализируя перемещения из расчета, к примеру, по МКЭ программе
Чем дальше, тем меньше я понимаю благородного дона :) В МКЭ программе я могу увидеть только конечные перемещения, направления же векторов ВОЗМОЖНЫХ перемещений анализируются ДО НАГРУЗОЧНЫХ ДЕФОРМАЦИЙ.
Это предположение верно лишь для нулевого подкоса. Для стойки оно не может быть верным, иначе узел раздвоится. Это видно из простейшего анализа деформированной схемы.
А может узел останется единым, а вот деформируются оба элемента?:)
P.S.Вообще то изменяемость, в том числе и мгновенная, анализируется по всем возможным направлениям во вне зависимости от конкретной нагрузки.