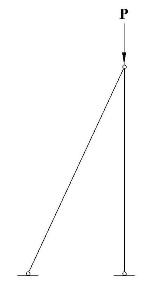
Есть элементарнейшая система из 2-х шарнирных элементов, один из которых вертикален, а другой расположен под некоторым углом, так как показано на рисунке. Внизу оба стержня имеют шарнирно-неподвижные опоры, а в верхней точке системы приложена вертикальная сила. Данная система является неизменяемой и статически определимой: 3К-Ш=3*1-(1+1+1)=0. Составляя уравнения равновесия для верхнего узла, получаем, что усилие в стойке равняется внешней силе, а усилие в подкосе нулевое. Проверяем данный результат по программе – все наши выводы подтверждаются, то есть все верно.
Верно? А как же совместность деформаций и закон Гука? А если угол примыкания подкоса совсем малый, все равно ноль? Так будет или нет усилие в подкосе? Если будет, то… читай заголовок, если не будет, то почему?



Комментарии
Авторизоваться
Если в программе решать задачу ...
Данный аргумент принять не могу, ведь если в программу заложены лже-посылы, то и на выходе неизбежно будут получены лже-результаты :).
Если в программе решать задачу в геометрически нелинейной постановке, то при P = 1 тс усилие в стойке будет -1.00006 тс, усилие в подкосе (а подкос наклонён под углом 45 градусов) - 8.73685e-005 тс, это не ноль, что качественно и было показано в п. 61.
Методы строительной механики позволяют вычислять усилия с достаточной (погрешность - менее 1/100 процента) точностью, строительная механика - не лженаука.
Но вопрос остаётся: почему в программе, которая учитывает и находит перемещения узлов, нет усилия в подкосе?
Ответ в заголовке :))
То, что в подкосе есть усилие и подкос удлиняется - это уже доказанное утверждение в нашем обсуждении?
Пока здесь присутствуют только голословные высказывания, в том числе и с моей стороны. Хотелось бы математики, что ли ...
P.S. Как, видимо, всем понятно - вопрос вполне себе провакационный. Поэтому я спорю со всеми, ожидая все-же полного математически аргументированного ответа. Докажите на приведенном примере научность/ненаучность дисциплине "дилетанту" :)
В данной системе нет ничего, кроме продольных сил, но если выполнить расчет по программе, то перемещения однозначно будут. Более того, именно перемещения в МКЭ первичны (вычисляются из системы линейных уравнений), а уж по ним вычисляются все усилия.
Согласен. Но вопрос остаётся: почему в программе, которая учитывает и находит перемещения узлов, нет усилия в подкосе? Моё предположение: программа составила уравнения равновесия для недеформированной схемы, далее составила уравнения, отражающией закон Гука и уравнения совместности деформаций. Решение системы уравнений отражает тот факт, что уравнения равновесия составлялись для недеформированной схемы.
То, что в подкосе есть усилие и подкос удлиняется - это уже доказанное утверждение в нашем обсуждении?
Расчётные программы устроены так, что, как и в ручном расчёте, при рассмотрении статически определимых конструкций перемещения узлов, вызванные осевыми деформациями стержней, при определении усилий в стержневых элементах не учитываются
Ну, это совсем не так :) Все программы учитывают интегралы Мора в части изгибающих и крутящих моментов и продольных сил в любом случае. А тот же Скад имеет опцию включения в упомянутый интеграл и сдвиговых компонентов.
В данной системе нет ничего, кроме продольных сил, но если выполнить расчет по программе, то перемещения однозначно будут. Более того, именно перемещения в МКЭ первичны (вычисляются из системы линейных уравнений), а уж по ним вычисляются все усилия.
И какой же вывод?
Расчётные программы устроены так, что, как и в ручном расчёте, при рассмотрении статически определимых конструкций перемещения узлов, вызванные осевыми деформациями стержней, при определении усилий в стержневых элементах не учитываются. Это может быть вызвано тем, что уравнения равновесия в расчётной программе, как и в ручном расчёте, составляются для недеформированной схемы.
Есть расчётные программы, которые вообще не учитывают осевые деформации стержней, например "Полюс" (http://dwg.ru/dnl/3464) - в ней перемещение верхнего узла равно нулю, а если добавить второй подкос с другой стороны, то выдаётся сообщение о том, что "невозможно решить фундаментальное уравнение".
Получилось противоречие вызванного неверным предположением в начале рассуждения. Значит, длина подкоса изменяется.
Почему в программах с МКЭ нулевое усилие в подкосе - не знаю.
И какой же вывод?
Если длина подкоса не изменилась после нагружения, то в подкосе нет осевых усилий, а значит опорные реакции подкоса - нулевые (т.к. тело, к которому приложены две силы, находится в равновесии, если силы равны и направлены навстречу, то есть поперечной к оси стержня составляющей реакции подкоса тоже нет), тогда верхний узел находится под действием двух сил - опорной реакции стойки, направленной вдоль стойки, и внешней силы Р. Раз верхний узел сместился по горизонтали (т.к. он сместился в силу упругости стержней, а сместится строго по горизонтали не может из-за поворота подкоса без осевой деформации), то верхний узел находится под действием двух сил - одна - Р - вертикальна, а вторая - опорная реакция стойки - наклонена под некоторым углом к вертикали. При ненулевых силах узел находиться в равновесии не может - одна из сил даёт ненулевую проекцию на горизонтальную ось, а вторая - не даёт.
Получилось противоречие вызванного неверным предположением в начале рассуждения. Значит, длина подкоса изменяется.
Почему ручной расчёт статически определимой конструкции и расчёт в программе с МКЭ указывают нулевое усилие в подкосе? Удлинение подкоса мало, перемещение верхнего узла мало, на запись уравнений равновесия смещение узла не влияет. Почему в программах с МКЭ нулевое усилие в подкосе - не знаю.
Как определить аналитически удлинение подкоса? Есть две неизвестные величины - удлинения подкоса и стойки. Выражаем через них смещение верхнего узла. С учётом этого смещения записываем уравнения равновесия для верхнего узла. Находим усилия в стержнях. Вычисляем удлинения стержней.
подкос будет иметь нулевые усилия, до момента "складывания" схемы.При условии что сила Р направлена вдоль оси стойки в любой момент времени.
Считаем, что сила имеет гравитационную природу и не является следящей.
Цитата:
Сообщение #57 от KACKADEP
Этот момент наступает тогда, когда деформации вертикальной стойки достигнут величины dx=b+c-а (Или угол между горизонталью и подкосом будет равен 0),
Намного раньше вся система "сломается".
Если не трудно поясните?
Цитата:
Сообщение #57 от KACKADEP
При составлении уравнения равновесия мы получаем, что вертикальная стойка воспринимает на себя всю нагрузку P...
Повторяюсь, именно этот и момент и "оспаривается" :)
Возможно ответ уже был в комментариях, просто не вижу проблем с совместностью деформаций и законом Гука, подкос будет иметь нулевые усилия, до момента "складывания" схемы.При условии что сила Р направлена вдоль оси стойки в любой момент времени.
Вопрос: какие усилия возникнут в стержнях? Понятно, что необходимо найти реакции опор, чтобы ответить на него.
Данная схема внешне статически неопределимая, поэтому про вертикальные опорные реакции кронштейна можно сказать только, что их сумма равна внешней нагрузке, а горизонтальные реакции исходной схемы равны по величине и противоположны по направлению :). Решение для данных схем возможно только путем рассмотрения равновесия нагруженного узла. Но именно это и сделано в исходной схеме, и выражено сомнение о корректности такого подхода.
Этот момент наступает тогда, когда деформации вертикальной стойки достигнут величины dx=b+c-а (Или угол между горизонталью и подкосом будет равен 0),
Намного раньше вся система "сломается".
При составлении уравнения равновесия мы получаем, что вертикальная стойка воспринимает на себя всю нагрузку P...
Повторяюсь, именно этот и момент и "оспаривается" :)
это требует доказательства
Предлагаю зайти "с тылу" :) Применим инженерный подход.
Повернем рассматриваемую систему на 90 градусов. Превратим ее в кронштейн. Загрузим той же вертикальной силой. Вопрос: какие усилия возникнут в стержнях? Понятно, что необходимо найти реакции опор, чтобы ответить на него. Получится, что в горизонтальном стержне опорная реакция горизонтальна, сонаправлена с осью стержня, нормальна к вертикали. Вертикальная реакция в данном узле отсутствует, проекция продольного усилия в стержне на вертикаль равна нулю. Почему? потому, что угол 90 градусов, а косинус угла 90 градусов равен нулю. Рассматриваем опору наклонного стержня. Неважно вверх он напрвлен или вниз относительно горизонтального. Если вниз - будет сжат, если вверх - растянут. Реакция в опоре вертикальная, очевидно, будет равна внешней действующей силе, из условия равновесия. Реакция горизонтальная будет пропорциональна соотношению рычагов внешней силы относительно опоры (длина горизонтального стержня) и величине разноса точек опоры (расстояние между опорными узлами по вертикали). [Offtop: как же тяжело без картинок] Из условия равновесия горизонтальная реакция в опоре горизонтального стержня равна только что вычисленной, с обратным знаком.
К чему это я все написал? Возвращаемся к нашей первоначальной задаче. Вычисляем опорные реакции в нашей системе. Очевидно, что реакция в опоре вертикального стержня только одна - вертикальная, величина ее равна внешней силе и обратна по направлению действия. А что с реакциями в опоре наклонного стержня? А нет их там - нет горизонтальных сил, значит нет горизонтальных реакций. И вертикальных тоже нет, из условия равновесия весь их запас "уже растрачен" на опору под вертикальным стержнем. Вот если бы этот стержень отклонить от вертикали, хоть на чуть-чуть! Тогда появится "игра сил".
Ну, а раз опорные реакции обе равны нулю, значит и усилие в наклонном стержне равно нулю.
Вот только теперь самое интересное начинается, стержень то вертикальный под действием силы укоротился. (При условии, что у него есть своя, конечная жесткость, что он не абсолютно жесткий). Значит наклонному стержню, чтобы сохранить свою длину неизменной необходимо отклониться по горизонтали. Ну, а если он отклонится - значит должны в нем возникнуть усилия, зря что-ли все выше было написано? В этом и заключается отличие расчетов в линейной постановке и нелинейной, в моем понимании. Ну, а дальше, я думаю автор меня поправит с точки зрения методически правильного объяснения. Ну или направит... в нужную сторону. Прошу прощения за столь длинное послание. Как-то непривычно в таком формате общаться - на форуме-то все понятно, а здесь в чужом блоге, как-то неудобно получается.
При ее отсутствии - стержни будут поворачиваться без возникновения усилия в подкосе.
Возможно :), но это требует доказательства с выкладками, пусть и из условия не деформированной схемы (не путать с не учетом деформаций).
Вообще же эта тема наглядно демонстрирует то, что порой ой как не просто доказать очевидные вещи, особенно, если с другой стороны выступает пройдоха-адвокат, не чурающийся любых методов доказательств :))
Эту задачу решают...
Сорри, только сейчас увидел, что уже несколько страниц написано :(
По теме - все мои выкладки справедливы при наличии горизонтальной связи в верхнем узле. При ее отсутствии - стержни будут поворачиваться без возникновения усилия в подкосе.