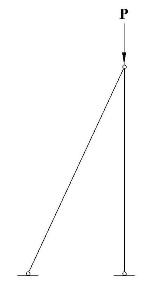
Есть элементарнейшая система из 2-х шарнирных элементов, один из которых вертикален, а другой расположен под некоторым углом, так как показано на рисунке. Внизу оба стержня имеют шарнирно-неподвижные опоры, а в верхней точке системы приложена вертикальная сила. Данная система является неизменяемой и статически определимой: 3К-Ш=3*1-(1+1+1)=0. Составляя уравнения равновесия для верхнего узла, получаем, что усилие в стойке равняется внешней силе, а усилие в подкосе нулевое. Проверяем данный результат по программе – все наши выводы подтверждаются, то есть все верно.
Верно? А как же совместность деформаций и закон Гука? А если угол примыкания подкоса совсем малый, все равно ноль? Так будет или нет усилие в подкосе? Если будет, то… читай заголовок, если не будет, то почему?



Комментарии
Авторизоваться
Лучше докажите, что в Вашем треугольнике, нагруженном соответствующим образом, не может возникнуть очень малых перемещений при нулевых деформациях подкоса. Пока же очевидно(не только для меня, кстати), что Ваш треугольник, с углами, не стремящимися к нулю, на мгновение становится подобием паровой машины.
Так Вы и вправду всерьез? Да-а-а-уж :(
Ну хорошо. Открываем любую книгу по строймеху, хоть для техникумов. Находим раздел анализа статической неизменяемости плоских сооружений. Одной из первых мы увидим пример неизменяемой системы, где узел (верхняя точка нашего треугольника) и диск (земля) соединены двумя не параллельными стержнями (стойка и раскос). Кое-где написано, что такая система называется диадой. К этой неизменяемой системе аналогичным образом можно присоединить еще одну точку, потом к получившейся системе еще одну ...
Признаком же мгновенной изменяемости является временное (до перемещений) совпадение векторов возможных перемещений в точке соединения элементов. Например, в случае шарнирно опертой однопролетной балки с промежуточном шарниром, векторы возможных перемещений в нем для обоих сходящихся элементов до начала деформаций будут направлены вертикально вниз или вверх.
Ничего подобного в предложенной схеме мы не наблюдаем: вектора возможных начальных перемещений направлены к каждому из элементов под углом в 90 градусов и составляют соответственно между собой угол равный углу наклона подкоса к стойке.
Прошу Вас, IBZ, определите по ней усилия в вертикальном и горизонтальных элементах своей формулой, а затем правильно.
Да где уж мне, я вот один треугольник осилить не могу, а тута их аж два :)), да и формулы никакой я не знаю :(
Если шарнирный треугольник с углами, не стремящимися к нулю, есть мгновенно изменяемая система, то..., то..., то..., одним словом, я плакаль :(
Ну что Вы, бросьте, к чему все эти слезы? Лучше докажите, что в Вашем треугольнике, нагруженном соответствующим образом, не может возникнуть очень малых перемещений при нулевых деформациях подкоса. Пока же очевидно(не только для меня, кстати), что Ваш треугольник, с углами, не стремящимися к нулю, на мгновение становится подобием паровой машины.
Вот https://cloud.mail.ru/public/21GhKj2WoAGx/МИС_треугольники.png еще схемку из треугольников, обладающую свойством МИС, сочинил. Прошу Вас, IBZ, определите по ней усилия в вертикальном и горизонтальных элементах своей формулой, а затем правильно.
икаких "погодьте" и "уважаемый"! Только "благородный дон" и "будьте любезны, помедленнее" :))).
"Прощенья просим, благородный дон, обознались, ошибочка произошла. ... Нежелательно бы нам, чтобы жалобы у вас были, благородный дон..." (c) :))
Вы решаете систему обладающую свойством мгновенной изменяемости, как неизменяемую систему, а затем ставите под сомнение результат. Мгновенно изменяемая система – система, в которой могут возникать малые перемещения без деформации её элементов. Вот Вы заявляете, что шарнирный треугольник ни при каких условиях не может быть МИС. Ну, будьте последовательны, докажите это перед тем, как применять 3К-Ш и т.п.
Если шарнирный треугольник с углами, не стремящимися к нулю, есть мгновенно изменяемая система, то..., то..., то..., одним словом, я плакаль :(
Погодьте, погодьте, уважаемый дон :).
Никаких "погодьте" и "уважаемый"! Только "благородный дон" и "будьте любезны, помедленнее" :))).
Именно Ваш постулат про нулевой подкос и поставлен под "сомнение" в исходном тексте.
Ничего подобного, это не мой постулат, а Ваш. И вот почему. Вы решаете систему обладающую свойством мгновенной изменяемости, как неизменяемую систему, а затем ставите под сомнение результат. В чем великий смысл сего пассажа? Напомню вам из курса строймеха, что значит МИС.
Мгновенно изменяемая система – система, в которой могут возникать малые перемещения без деформации её элементов. Вот Вы заявляете, что шарнирный треугольник ни при каких условиях не может быть МИС. Ну, будьте последовательны, докажите это перед тем, как применять 3К-Ш и т.п.
Любая МКЭ программа это, кстати, обязательно учитывает и в линейной постановке.
МКЭ программа не учитывает это. Программа решает вариационную задачу отыскания перемещений, удовлетворяющих всем совместностям исходя из всем известных принципов. А затем на найденых перемещениях отыскивает усилия. Я же, исходя из не полностью поставленных Вами начальных условий и методов расчета, пошел наоборот, от усилий к деформациям и перемешениям. Не вижу в этом ничего противозаконного и не очевидного.
Только вот я никакой очевидности в повороте раскоса БЕЗ ДЕФОРМАЦИЙ не вижу.
Для начала увидьте признаки МИС в вашей системе, сразу станет очевидным поворот. Ведь строймех ни от кого не скрывает, что МИС и т.п. системы могут быть правильно решены только из рассмотрения совместных деформаций и перемещений. Это же очевидно, не так ли?
Считаю, что необходимым и достаточным доказательством может служить математическая запись факта, что длина раскоса осталась при любых смещениях прежней. Ну или что-то столь же наглядное :)
Ну, а мат. запись благородного дона для Вас, конечно же, не является достаточным доказательством?:)))
Т.к. доказательство строится на расчете деформаций по усилиям, полученным из уравнений равновесия недеформированной схемы, имеем сжатую стойку и нулевой подкос. Другими словами подкос не укорачивается, а стойка укорачивается на, определенную из закона Гука, дельту. Следствием обязательной совместности перемещений общего для стойки и подкоса узла, а также нулевого укорочения подкоса является поворот и подкоса и стойки относительно собственных опорных шарниров на такой угол, который будет обеспечивать выполнение закона Гука и для стойки и подкоса.
Погодьте, погодьте, уважаемый дон :). Именно Ваш постулат про нулевой подкос и поставлен под "сомнение" в исходном тексте. Да, в данной системе при углах примыкания раскоса к стойке 0 < a < 90 (другие четверти не рассматриваем) обязательно будут смещения по X, Z, и, соответственно, угол поворота. Любая МКЭ программа это, кстати, обязательно учитывает и в линейной постановке. Только вот я никакой очевидности в повороте раскоса БЕЗ ДЕФОРМАЦИЙ не вижу. Считаю, что необходимым и достаточным доказательством может служить математическая запись факта, что длина раскоса осталась при любых смещениях прежней. Ну или что-то столь же наглядное :)
при этом: dB=B-L';
Пусть будет вертикальным перемещение X
получается L'=B-X или нет?
румата: Из подобия треугольников: S/A=X/C=Y/B; Y=Q*B; X=Q*C
по какому признаку они подобны?
Ваше предположение можно будет считать верным, если Вы докажете его аналитически, так как любая сумма примеров доказательством считаться не может.
Вообще, для этого в условии задачи все же нужно бы обозначить соотношение жесткостей подкоса и стойки, а также пределы теории расчета.
Ну, допустим жесткости конечны, равны, а результирующие деформации/перемещения малы. Т.к. доказательство строится на расчете деформаций по усилиям, полученным из уравнений равновесия недеформированной схемы, имеем сжатую стойку и нулевой подкос. Другими словами подкос не укорачивается, а стойка укорачивается на, определенную из закона Гука, дельту. Следствием обязательной совместности перемещений общего для стойки и подкоса узла, а также нулевого укорочения подкоса является поворот и подкоса и стойки относительно собственных опорных шарниров на такой угол, который будет обеспечивать выполнение закона Гука и для стойки и подкоса.
Теперь, собственно, вывод аналитической связи между укорочением стойки и, ранее обозначенным, углом поворота:
Обозначим длину подкоса за А, длину стойки за В, а расстояние между опорными шарнирами за С. Имеем также некоторые перемещения общего узла, угол поворота стойки и подкоса и укорочение стойки. Обозначим перемещения за X и Y. Пусть будет вертикальным перемещение X, а горизонтальным - Y. Угол поворота обозначим - Q, а укорочение стойки - dB. Ввиду малости перемещений/деформаций имеем право уравнять длину дуги окружности подкоса A на угле поворота Q хордой S.
Имеем: S=Q*A.
Из подобия треугольников: S/A=X/C=Y/B; Y=Q*B; X=Q*C
Из закона Гука знаем чему равно dB, при этом: dB=B-L';
Из теоремы Пифагора: L'=sqrt((B-X)^2+Y^2)
Переписываем итоговую зависимость: dB=B-sqrt((B-Q*C)^2+(Q*B)^2)
Вы деформации или, хотя бы, перемещение нагруженного узла вычисляли? Могу предположить, что не вычисляли.
Ваше предположение не верно :)
Иначе Вы бы поняли, что, в данном случае, укорачивается только вертикальный стержень, а длина наклонного остается неизменной и после загружения. Он просто поворачивается вокруг своего опорного узла.
Ваше предположение можно будет считать верным, если Вы докажете его аналитически, так как любая сумма примеров доказательством считаться не может. Пока никаких деформированных схем (в смысле итерационного учета нелинейности) не рассматриваем, это попозже :)
Дело в этой системе не в жесткостях и не в точности методов расчета, а в самой системе ... стандартная мгновенно изменяемая система...
Вот тебе и на, с каких это пор шарнирный треугольник стал мгновенно изменяемым ???
1. Формула Чебышева для нахождения лишних связей Л=2Ш+С0-3Д
Дык я, вроде, об этом и не спрашивал. Сам предпочитаю применять формулу Л=3*K-Ш, о применении которой можно почитать тут: http://forum.dwg.ru/showthread.php?t=45482&page=4&highlight;= пост 74. Хм, прямую ссылку вставить здесь, похоже, нельзя? Ага, уже можно - спасибо Админу за оперативность!
Второй пункт цитируемого сообщения пока оставлю без коментариев ... Хотя я, признаться, несколько удивлен участию в обсуждении "доцентов с кандидатами" (c).
А насчет названия темы - так это чистый плагиат :) Именно такую фразу я достаточно часто слышал от своего бывшего начальника. А к нему я всегда прислушивался, так как это единственный знакомый мне специалист, время от времени использовавший дифуры и интегралы при реальных расчетах :)) Благо образование позволяло: мехмат + строительный.
P.S. Вообще то иногда вопросы задают, зная при этом ответ. Ну так, интересно кто чего скажет :)
2. Если мы рассматриваем идеализированные стержни в статической постановке задачи (без учета веса конструкций, температурных дел, неточности монтажа и т.д.), то подкос будет иметь не нулевые значения только в двух случаях: направляющая подкоса к направляющей вертикального элемента оставляет угол 0 и 180 градусов соответственно, если отсчет принять за шарнир, к которому приходит сила и помним еще, что при угле в 0гр, наша система переход в «систему неустойчивую в большем». Если мы рассматриваем «более-менее» реалистичную постановку задачи (собственный вес, эксцентриситеты и нагрузки вызванные деформациями (перемещением) от внешних сил, реальные геометрические и физические характеристики (площадь, модуль упругости и т.д.) , то усилия будут. Маленькие, но будут. А какие по знаку и величине нужно считать для каждого конкретного случая. Учитывать- не учитывать в расчетах эти усилия – каждый решает сам. Для примера можно глянуть Тимошенко «Сопротивление материалов» 1960г.,Т.1 стр.19-21 (необходимо немного подкорректировать задачи 3-5) и не забывать про «уловку» см. Феодосьев «Избранные задачи и вопросы по сопротивлению материалов» 1967г., стр. 7, задача 1.
3. Вроде ответил на ваши вопросы. И с вашего позволения задам вам вопрос: «Что значит строймеханика- лженаука?» Просто интересно стало:)
а чего его ловить. делаете расчет в два шага. на втором шаге явно увидите растяжение
румата: Никакого растяжения за один шаг решения быть не может
вы ведь про первый шаг это написали. вот и предложите расчетную схему первого шага, на котором сжатие, я думаю, что сумма проекций сил на горизонтальную ось, у вас, не будет равна нулю. а про второй шаг с растяжением и так все понятно.
Сообщение #24 от efwl
речь шла о деформированной системе
румата: ничего подобного, речь шла о линейном расчете (т.е. о расчете за один шаг)
вот и посмотрим на этот один- первый шаг
тут вообще не о количестве шагов, а о том- учитываем влияние деформаций или нет
а если речь зашла о повороте, в результате уменьшения длины вертикального стержня, то в этом случае деформ. учитываются
речь шла о деформированной системе
ничего подобного, речь шла о линейном расчете (т.е. о расчете за один шаг)
да ну,
попробуйте поймать этот шаг
а чего его ловить. делаете расчет в два шага. на втором шаге явно увидите растяжение, если правильно составите уравнения равновесия на деформированной схеме.
Цитата:Сообщение #20 от efwlтак это был намек на то, что он растянутый- вот как
Это Вы о чем?. Никаких намеков не было. Никакого растяжения за один шаг решения быть не может. Впрочем как и глобально верного результата.
речь шла о деформированной системе
румата: Никакого растяжения за один шаг решения быть не может
да ну,
попробуйте поймать этот шаг, когда там (в наклонном ст.) сжатие. если, условно, силу Р разделить между двумя стержнями, то в наклонном стержне появится гориз. составляющая, которая и вызывает поворот, но это мгновенно происходит